2 定義
双曲線関数とは、次のように定義されるものである。
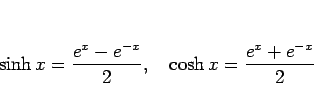 |
(1) |
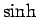 は「ハイパボリックサイン」、
は「ハイパボリックサイン」、
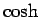 は「ハイパボリックコサイン」と読む 4 文字の関数名である。
ハイパボリック (hyperbolic) とは、
「ハイパーボラ (hyperbola)
は「ハイパボリックコサイン」と読む 4 文字の関数名である。
ハイパボリック (hyperbolic) とは、
「ハイパーボラ (hyperbola) 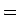 双曲線」という言葉の形容詞形で、
「双曲的な」という言葉を指している。
そのため、双曲線関数と呼ばれるのであるが、
この「双曲的」という言葉がなぜついているのかについては、
3 節で紹介する。
双曲線」という言葉の形容詞形で、
「双曲的な」という言葉を指している。
そのため、双曲線関数と呼ばれるのであるが、
この「双曲的」という言葉がなぜついているのかについては、
3 節で紹介する。
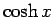 は
は
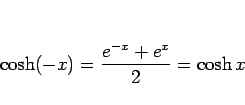 |
(2) |
より偶関数、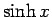 は、
は、
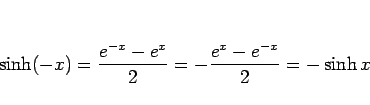 |
(3) |
より奇関数である。
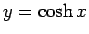 ,
, 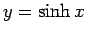 のグラフは、
のグラフは、
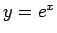 ,
, 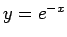 のグラフから容易にわかるが、
図 1 のようになる。
のグラフから容易にわかるが、
図 1 のようになる。
図 1:
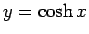 ,
,
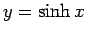 のグラフ
のグラフ
|
|
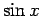 ,
, 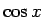 以外の三角関数が、
以外の三角関数が、

と定義されるのと同様に、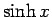 ,
, 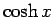 以外の双曲線関数は、
以外の双曲線関数は、
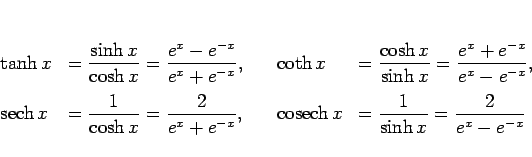 |
(4) |
と定義される。
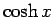 ,
, 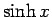 以外でよく用いられるのは
以外でよく用いられるのは 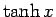 程度であり、
程度であり、
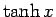 ,
, 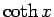 のグラフは図 2 のようになる。
のグラフは図 2 のようになる。
図 2:
 ,
,
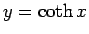 のグラフ
のグラフ
|
|
なお、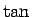 (タンジェント)、
(タンジェント)、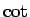 (コタンジェント) は、
特に東欧では tg, ctg のように書かれることも多い。
その流儀では、
(コタンジェント) は、
特に東欧では tg, ctg のように書かれることも多い。
その流儀では、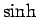 ,
, 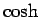 ,
, 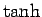 ,
, 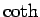 なども、
sh, ch, th, cth のように書かれるようである (例えば [2] 参照)。
なども、
sh, ch, th, cth のように書かれるようである (例えば [2] 参照)。
次の式は、双曲線関数の最も基本的な性質である。
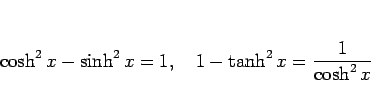 |
(5) |
なお三角関数と同様に、自然数 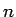 に対し、
に対し、
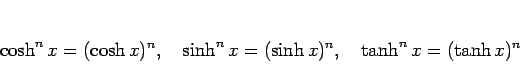
のように書くことになっている。
(5) の最初の式は、
定義の式 (1) を代入して展開すれば容易に得られるし、
2 本目の式は最初の式の両辺を 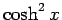 で割れば得られる。
で割れば得られる。
この性質 (5) は、三角関数の性質
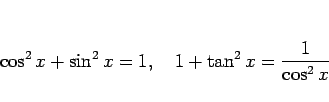
に対応している。
竹野茂治@新潟工科大学
2010年3月19日
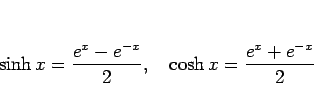
![]() は
は
![]() ,
, ![]() のグラフは、
のグラフは、
![]() ,
, ![]() のグラフから容易にわかるが、
図 1 のようになる。
のグラフから容易にわかるが、
図 1 のようになる。
![]() ,
, ![]() 以外の三角関数が、
以外の三角関数が、
![]() (タンジェント)、
(タンジェント)、![]() (コタンジェント) は、
特に東欧では tg, ctg のように書かれることも多い。
その流儀では、
(コタンジェント) は、
特に東欧では tg, ctg のように書かれることも多い。
その流儀では、![]() ,
, ![]() ,
, ![]() ,
, ![]() なども、
sh, ch, th, cth のように書かれるようである (例えば [2] 参照)。
なども、
sh, ch, th, cth のように書かれるようである (例えば [2] 参照)。
![]() で割れば得られる。
で割れば得られる。