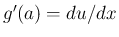 は
は 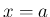 での
での 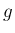 の変化率、すなわち
の変化率、すなわち 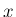 の 1 の
変化に対する
の 1 の
変化に対する 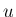 の変化を意味する。
の変化を意味する。
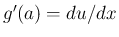 は
は 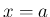 での
での 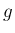 の変化率、すなわち
の変化率、すなわち 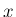 の 1 の
変化に対する
の 1 の
変化に対する 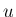 の変化を意味する。
の変化を意味する。
例えば、ある鉄の棒を熱したとき、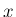 を熱した時間[秒]、
を熱した時間[秒]、
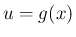 をそのときの温度[度] とすると、
をそのときの温度[度] とすると、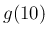 は 10 秒後の温度、
は 10 秒後の温度、
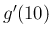 は 10 秒経過時点での、1 秒当たりの温度上昇、を意味する。
だから
は 10 秒経過時点での、1 秒当たりの温度上昇、を意味する。
だから 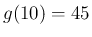 ,
, 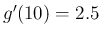 であれば、10 秒後は 45 度で、
10 秒経過時点では 1 秒当たり 2.5度 (2.5度/秒) 温度が
上昇していることを意味し、
例えば 10.2 秒後は約 0.5 度上がり約 45.5度となる。
であれば、10 秒後は 45 度で、
10 秒経過時点では 1 秒当たり 2.5度 (2.5度/秒) 温度が
上昇していることを意味し、
例えば 10.2 秒後は約 0.5 度上がり約 45.5度となる。
そして 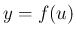 を温度
を温度 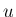 のときの棒の長さ[m] とすると、
合成関数
のときの棒の長さ[m] とすると、
合成関数 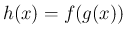 は、
は、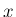 秒後の棒の長さとなる。
秒後の棒の長さとなる。
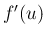 は温度
は温度 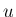 度のときの 1 度当たりの棒の伸びを意味し、
例えば
度のときの 1 度当たりの棒の伸びを意味し、
例えば 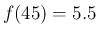 ,
, 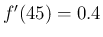 であれば、
温度 45度のときは 5.5m で、
温度 45度付近では、1 度温度が上昇すると 0.4m の割合で伸びる
ことになる (0.4m/度)。
であれば、
温度 45度のときは 5.5m で、
温度 45度付近では、1 度温度が上昇すると 0.4m の割合で伸びる
ことになる (0.4m/度)。
このとき、10 秒後の棒の長さは、
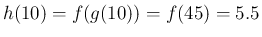 m で、
その 10 秒経過時点での棒の 1 秒当たりの伸び
m で、
その 10 秒経過時点での棒の 1 秒当たりの伸び 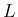 [m/秒] は、
1 秒当たり温度が 2.5 度上昇し、温度 1 度の上昇毎に棒は 0.4 m 伸びるので、
[m/秒] は、
1 秒当たり温度が 2.5 度上昇し、温度 1 度の上昇毎に棒は 0.4 m 伸びるので、
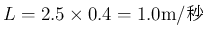
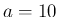 ,
, 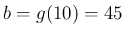 に対して
に対して
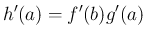
竹野茂治@新潟工科大学