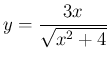 (5)
(5)
講義では、以下のような関数は合成関数とは見られないと例示した。
例えば、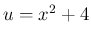 と置いても
と置いても 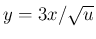 となって
となって 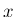 が
残ってしまうため、これは合成関数にはならない。
合成関数であるためには、
が
残ってしまうため、これは合成関数にはならない。
合成関数であるためには、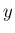 は
は 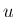 だけの関数でなければいけない。
だけの関数でなければいけない。
では、この関数は微分できないかと言えば、そうではなく、積の微分などと 組み合わせればちゃんと微分できる。 つまり、
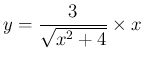
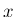 の積と見て、積の微分を先に適用すればよい。
まず、
と置くと
の積と見て、積の微分を先に適用すればよい。
まず、
と置くと 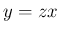 となる。ここで、
となる。ここで、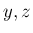 は
は 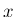 を変数とする関数
であることに注意する。積の微分により、
となる。次にこの
を変数とする関数
であることに注意する。積の微分により、
となる。次にこの 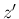 を求める。
を求める。
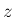 は (6) より合成関数で、
は (6) より合成関数で、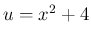 とすれば
とすれば
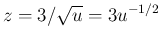 なので、合成関数の微分により、
なので、合成関数の微分により、
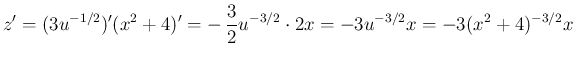
同様に、
も、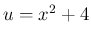 では
では 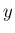 に
に 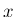 が残るので単純な合成関数ではないが、
合成関数が含まれる商と見ることで微分ができる。
が残るので単純な合成関数ではないが、
合成関数が含まれる商と見ることで微分ができる。
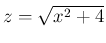 とすれば、
とすれば、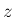 は合成関数で
は合成関数で 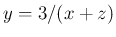 なので、
まず商の微分により、
となる。次は
なので、
まず商の微分により、
となる。次は 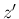 を求める。
を求める。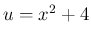 とすれば
とすれば
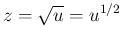 より、
より、
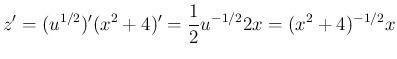
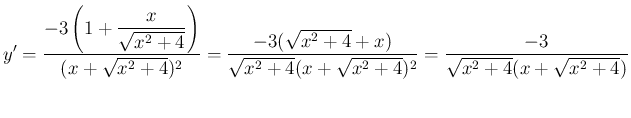
さらに、合成関数と合成関数の組み合わせもありうる。 例えば、
のような場合である。これも単純な合成関数ではなく、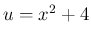 では、
では、
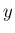 は
は 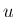 のみの関数にはならない。
この場合は、
のみの関数にはならない。
この場合は、
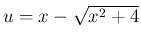 と置くと、
と置くと、
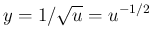 となり、
となり、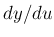 は難しくない。
ただし、
は難しくない。
ただし、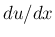 がまだ簡単には求まる形ではないが、
がまだ簡単には求まる形ではないが、
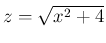 とすると、
とすると、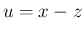 で、
で、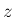 が合成関数なので、
が合成関数なので、
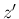 は別に合成関数の微分で求めることができる。
外側から順番に計算すると、合成関数の微分により
となる。
は別に合成関数の微分で求めることができる。
外側から順番に計算すると、合成関数の微分により
となる。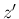 は、
は、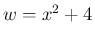 とすると
とすると
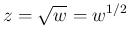 より
より
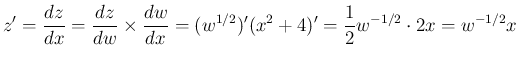
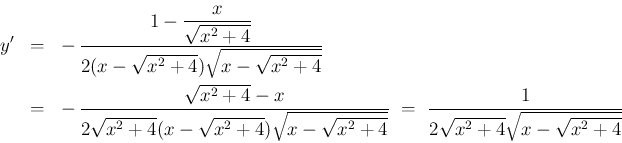
竹野茂治@新潟工科大学