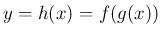 に対して、
に対して、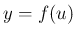 ,
, 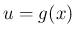 と
分けたときに、証明すべき公式 2.6 は
と
分けたときに、証明すべき公式 2.6 は
合成関数
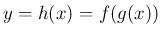 に対して、
に対して、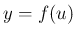 ,
, 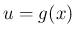 と
分けたときに、証明すべき公式 2.6 は
と
分けたときに、証明すべき公式 2.6 は
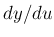 は
は 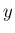 を
を 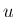 の関数として微分したもの、すなわち
の関数として微分したもの、すなわち 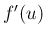 であり、
であり、
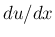 は
は 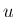 を
を 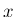 の関数として微分したもの、すなわち
の関数として微分したもの、すなわち 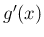 、
、
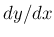 は
は 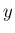 を
を 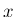 の関数として微分したもの、すなわち
の関数として微分したもの、すなわち 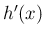 と
なるので、(1) と (2) は同じことを
意味することになる。
と
なるので、(1) と (2) は同じことを
意味することになる。
(2) のように書くのは、
これが分数の約分のように見えて覚えやすい形であるから、という理由もあるが、
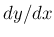 という記号は、少なくとも現代では「
という記号は、少なくとも現代では「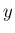 を
を 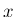 で微分したもの」を
意味する記号であり、「
で微分したもの」を
意味する記号であり、「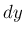 を
を 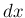 で割った商」ではなく、
「
で割った商」ではなく、
「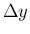 を
を 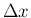 で割った商の極限 (0/0 の不定形の極限)」と
考えるので、直接その約分により (2) が証明される
わけではない。
で割った商の極限 (0/0 の不定形の極限)」と
考えるので、直接その約分により (2) が証明される
わけではない。
導関数は、極限によって、
と定義される。 ここで、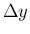 は、
は、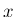 を
を 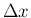 だけ増やしたときの
だけ増やしたときの 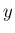 の
増加量 (「増分」) を意味し、式で書けば
の
増加量 (「増分」) を意味し、式で書けば
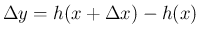
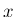 の
の 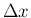 の変化に対する
の変化に対する 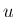 の増分
の増分 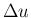 は
は
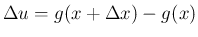
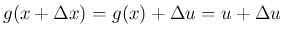
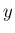 の増分
の増分 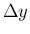 は、
は、
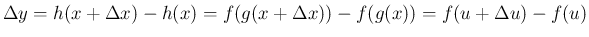
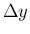 は、
は、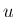 の変化量
の変化量 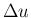 に
対する
に
対する 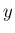 の増分と見ることもできる。これにより、
の増分と見ることもできる。これにより、
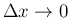 の際に、
当然
の際に、
当然
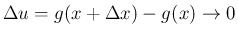 となるので、
よって (4) でその極限を考えれば
となるので、
よって (4) でその極限を考えれば
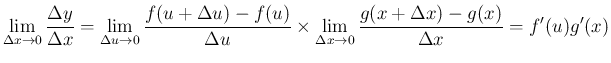
なお、(4) は、意味はわかりにくくなるが、 簡単に
竹野茂治@新潟工科大学