次へ: 4 最後に
上へ: '基礎数理 III 期末テスト (2006) の誤答等について'
前へ: 2.2 従属変数
(PDF ファイル: fortest2-2006.pdf)
色々目についた間違いを上げる。
zh
-
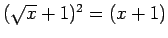 (正しくは
(正しくは
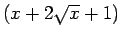 )
)
-
![$\displaystyle \frac{1}{\sqrt[3]{x}}=x^{3/2}$](img36.gif) や
や 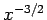 (正しくは
(正しくは 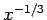 )
)
-
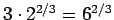 (積よりも累乗の方が優先順位は先なので、こんな計算はできない)
(積よりも累乗の方が優先順位は先なので、こんな計算はできない)
-
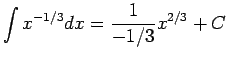 (正しくは
(正しくは
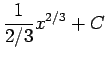 )
)
-
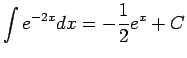 (正しくは
(正しくは
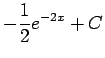 )
)
-
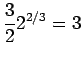
-
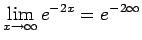 (この講義ではこのように書いてはいけない、とした)
(この講義ではこのように書いてはいけない、とした)
-
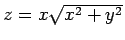 を
を 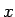 で偏微分するときに、
で偏微分するときに、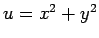 と置いて
と置いて
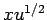 とし、これに合成関数の微分を使って
とし、これに合成関数の微分を使って
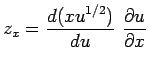 とするもの (
とするもの (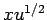 は
は 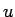 のみの式ではないから
のみの式ではないから
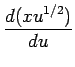 は意味がない)
は意味がない)
-
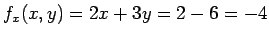
この最後のものは多少説明を要する。
これは接平面の問題に出てきた書き方であるが、
これ自体は正確に言えば間違いではないが、
一行省略していることによって接平面の公式との対応をわかりにくくしている
計算式である。
接平面の公式は、以下の通りである:
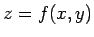 の、
の、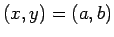 における接平面は、
における接平面は、
この式の 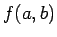 ,
, 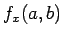 ,
, 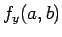 を求めて、
それらを代入すればよいのであるが、例えば、
を求めて、
それらを代入すればよいのであるが、例えば、
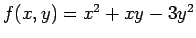 、
、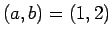 であるとしてこの問題を解く場合、
普通は、次のようにすると思う。
であるとしてこの問題を解く場合、
普通は、次のようにすると思う。
よって、これらを公式
に代入し、
しかし、答案では、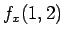 などの計算を以下のようにしているものが
いくつか見られた。
などの計算を以下のようにしているものが
いくつか見られた。
これらは、一旦 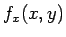 の式を求めた後で、
それに
の式を求めた後で、
それに 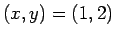 を代入して
を代入して 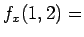 と書くのを
省略した書き方になっていて、
もし「
と書くのを
省略した書き方になっていて、
もし「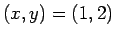 では」と断わっていれば一応間違いではないが、
このように書くと
では」と断わっていれば一応間違いではないが、
このように書くと 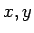 の式だったものが急に定数に変わるので、
やや紛らわしい。
の式だったものが急に定数に変わるので、
やや紛らわしい。
しかも求めたものが「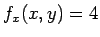 」のようになっているため、
元の接平面の公式に該当部分がない (公式の方は
」のようになっているため、
元の接平面の公式に該当部分がない (公式の方は 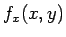 ではなくて
ではなくて
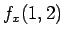 ) ので、中には公式の方を勝手に
) ので、中には公式の方を勝手に
のように書いているものまでいたが、この式は明らかに間違いである。
つまりこの式では、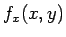 の
の 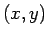 と
と 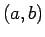 は別のものと
見なされるので、むしろ代入すべきは
は別のものと
見なされるので、むしろ代入すべきは 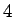 ではなくて
ではなくて
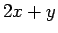 だということになってしまう。
だということになってしまう。
次へ: 4 最後に
上へ: '基礎数理 III 期末テスト (2006) の誤答等について'
前へ: 2.2 従属変数
竹野茂治@新潟工科大学
2006年8月31日
![$\displaystyle \frac{1}{\sqrt[3]{x}}=x^{3/2}$](img36.gif) や
や 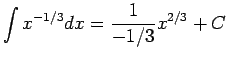 (正しくは
(正しくは
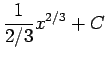 )
)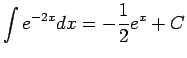 (正しくは
(正しくは
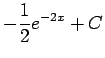 )
)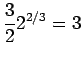
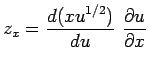 とするもの (
とするもの (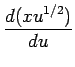 は意味がない)
は意味がない)![$\displaystyle \frac{1}{\sqrt[3]{x}}=x^{3/2}$](img36.gif) や
や 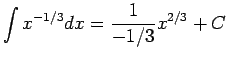 (正しくは
(正しくは
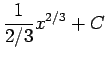 )
)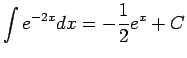 (正しくは
(正しくは
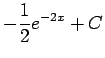 )
)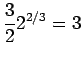
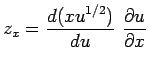 とするもの (
とするもの (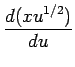 は意味がない)
は意味がない)の、
における接平面は、
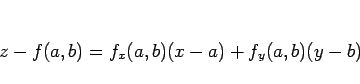
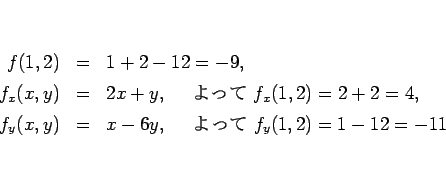
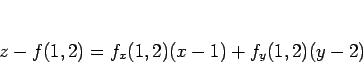
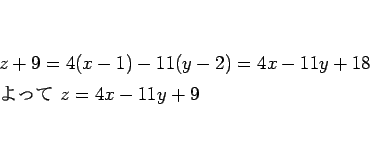
![]() などの計算を以下のようにしているものが
いくつか見られた。
などの計算を以下のようにしているものが
いくつか見られた。
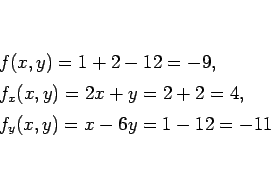
![]() 」のようになっているため、
元の接平面の公式に該当部分がない (公式の方は
」のようになっているため、
元の接平面の公式に該当部分がない (公式の方は ![]() ではなくて
ではなくて
![]() ) ので、中には公式の方を勝手に
) ので、中には公式の方を勝手に