次へ: 2.2 従属変数
上へ: 2 全般的な注意
前へ: 2 全般的な注意
(PDF ファイル: fortest2-2006.pdf)
まず、1. の 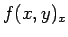 ,
, 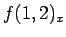 であるが、
これは書いた本人は
「
であるが、
これは書いた本人は
「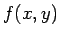 を
を 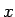 で偏微分したもの」、
「それに
で偏微分したもの」、
「それに 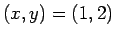 を代入したもの」
というつもりで書いたのだろうと思うが、
特に後の方の式それを表してはいない。
を代入したもの」
というつもりで書いたのだろうと思うが、
特に後の方の式それを表してはいない。
右下に偏微分を表す 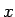 をつける場合、
その式の意味は、詳しく言えば次のようになる。
をつける場合、
その式の意味は、詳しく言えば次のようになる。
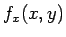 :
: 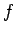 という名前の関数を、
それを元々定義していた式を
という名前の関数を、
それを元々定義していた式を 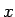 で偏微分して、
その式の最初の変数に
で偏微分して、
その式の最初の変数に 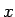 を、後の変数に
を、後の変数に 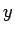 を代入したもの
を代入したもの
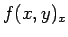 これは、
これは、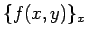 に等しく、
つまり、
に等しく、
つまり、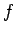 という名前の関数の
最初の変数に
という名前の関数の
最初の変数に 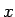 を、後の変数に
を、後の変数に 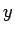 を代入したものを
を代入したものを
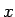 で偏微分したもの
で偏微分したもの
ということになる。前者は微分が先でその後に代入、
後者は代入が先でその後が微分、という点が異なる。
一変数関数の場合の 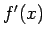 と
と 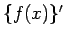 の関係と同じである。
の関係と同じである。
この場合、元々 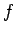 が
が 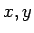 の式として定義されていたのなら問題はないが、
もし
の式として定義されていたのなら問題はないが、
もし 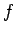 が最初に
が最初に
とでも定義されていたとすれば、両者の意味は異なることになる。
つまりこの場合、元々の定義式の言う 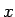 は第一変数ではなく
第二変数であるから、
は第一変数ではなく
第二変数であるから、
となるので、
となるが、
なので、
となってしまうからである。
今回の問題の場合は、元々 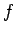 が
が 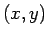 の式であったので、
このような誤解はないが、
の式であったので、
このような誤解はないが、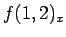 はどちらの場合でも明らかな間違いである。
すなわち、
はどちらの場合でも明らかな間違いである。
すなわち、
となるからである (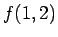 は定数)。
は定数)。
次へ: 2.2 従属変数
上へ: 2 全般的な注意
前へ: 2 全般的な注意
竹野茂治@新潟工科大学
2006年8月31日
![]() をつける場合、
その式の意味は、詳しく言えば次のようになる。
をつける場合、
その式の意味は、詳しく言えば次のようになる。
![]() が
が ![]() の式として定義されていたのなら問題はないが、
もし
の式として定義されていたのなら問題はないが、
もし ![]() が最初に
が最初に
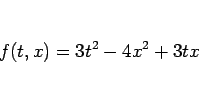
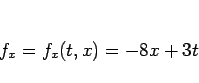
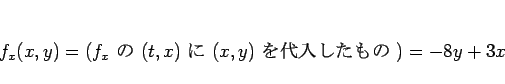

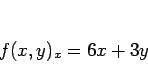
![]() が
が ![]() の式であったので、
このような誤解はないが、
の式であったので、
このような誤解はないが、![]() はどちらの場合でも明らかな間違いである。
すなわち、
はどちらの場合でも明らかな間違いである。
すなわち、