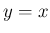
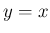 に関して対称という関係がある。
これを利用して、逆関数の微分をグラフを用いて考える方法もある。
今度はその方法で、例えば公式 3 から公式 4 を導いてみる。
に関して対称という関係がある。
これを利用して、逆関数の微分をグラフを用いて考える方法もある。
今度はその方法で、例えば公式 3 から公式 4 を導いてみる。
今、
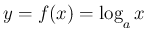 とし、公式 3 を仮定した上で
この関数の、
とし、公式 3 を仮定した上で
この関数の、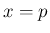 での微分係数
での微分係数 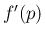 を求める。
を求める。
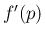 は、この関数のグラフの
は、この関数のグラフの
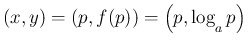 でのグラフの傾きであることに注意する。
でのグラフの傾きであることに注意する。
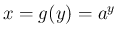 のグラフ
になる (図 1)。
先程の点は、そのグラフの
のグラフ
になる (図 1)。
先程の点は、そのグラフの
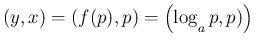 に
対応し、
に
対応し、
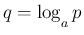 とすると
とすると 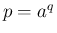 で、
で、
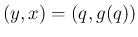 となる。
その点での
となる。
その点での 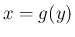 のグラフの傾きは、公式 3 より、
となるが、
のグラフの傾きは、公式 3 より、
となるが、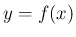 のグラフと
のグラフと 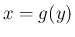 のグラフは
軸の縦と横を入れ替えたものなので、
のグラフは
軸の縦と横を入れ替えたものなので、
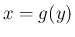 のグラフの
のグラフの
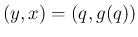 での傾き
での傾き 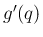 、
すなわち横方向の
、
すなわち横方向の 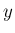 方向に 1 進むときに縦方向の
方向に 1 進むときに縦方向の 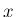 方向に
方向に 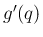 上がる
傾きは、
上がる
傾きは、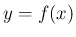 のグラフの
のグラフの
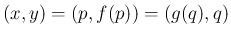 では、
横方向の
では、
横方向の 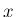 方向に
方向に 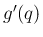 進むときに
縦方向の
進むときに
縦方向の 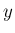 方向に 1 上がる傾き
方向に 1 上がる傾き 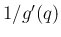 に変わり (図 2)、
それが
に変わり (図 2)、
それが 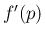 に等しいので、よって
に等しいので、よって
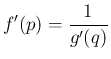
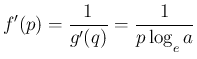
竹野茂治@新潟工科大学