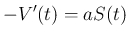 (1)
(1)
雪玉が法則に従ってとけていくと、段々表面積が小さくなっていくので、
とける速さも徐々に遅くなるが、
最終的には 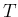 分後に完全にとけて
分後に完全にとけて 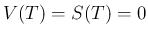 となることが予想される。
となることが予想される。
実際にその 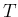 の値、および途中の
の値、および途中の 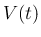 がどのような式で表されるのかも、
実は (1) から求めることができる。
物理法則を元に微分を使った式を立てることにより
がどのような式で表されるのかも、
実は (1) から求めることができる。
物理法則を元に微分を使った式を立てることにより 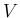 と
と 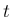 の完全な関係式を求められることが、
微分の大きな力であり、
そしてそのことによって微積分成立以後の科学は大きく発展したとも言える。
(1) のような未知関数 (今の場合は
の完全な関係式を求められることが、
微分の大きな力であり、
そしてそのことによって微積分成立以後の科学は大きく発展したとも言える。
(1) のような未知関数 (今の場合は 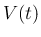 や
や 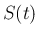 ) に
対する微分の関係式を「微分方程式」と呼ぶ。
) に
対する微分の関係式を「微分方程式」と呼ぶ。
この微分方程式 (1) を解いて 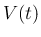 を
を 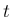 の式で表してみよう。
まず、(1) から
の式で表してみよう。
まず、(1) から 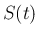 を消去して
を消去して 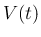 だけの式にする。
雪玉が球体のまま小さくなると仮定し、その半径を
だけの式にする。
雪玉が球体のまま小さくなると仮定し、その半径を 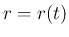 とすると、
とすると、
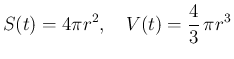
今、
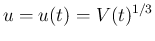 とすると、
合成関数の微分により、
とすると、
合成関数の微分により、
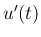 は定数となる。
よって
は定数となる。
よって 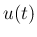 は
は 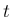 の一次式で、
の一次式で、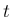 の係数は
の係数は 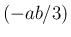 となる。
となる。
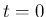 では
では
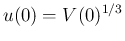 なので、結局
となり、
なので、結局
となり、
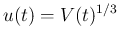 より
となることがわかる。これで
より
となることがわかる。これで 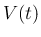 を表す式が得られた。
を表す式が得られた。
また、雪玉がなくなる時刻 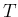 は、
は、
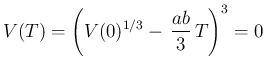
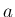 は、温度など環境によって変わるが、
実測、すなわち一定時間でどれくらい半径が減ったかを調べれば
求めることはできる。
は、温度など環境によって変わるが、
実測、すなわち一定時間でどれくらい半径が減ったかを調べれば
求めることはできる。
例えば、半径が 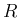 [cm] のときに、半径が
[cm] のときに、半径が 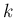 [cm/分] 減って
いたとする (半径の減少を 1 分当たりに直した値)。
このとき、半径が
[cm/分] 減って
いたとする (半径の減少を 1 分当たりに直した値)。
このとき、半径が 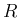 のときの時刻を
のときの時刻を 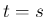 とすると、
とすると、
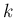 は
は 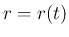 の
の 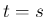 での減少率だから、
での減少率だから、
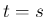 とすれば (9) より
とすれば (9) より
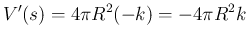
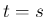 とすれば、
とすれば、
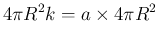
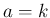 となる。
となる。
なお、(7) を 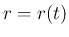 で表してみると、
で表してみると、
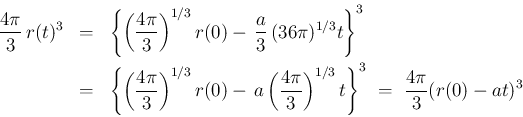
 の式はずっと易しくなる。
(11) から、または (8) からもわかるが、
の式はずっと易しくなる。
(11) から、または (8) からもわかるが、
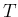 も
も 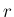 で表せば、
で表せば、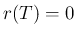 より
となる。
竹野茂治@新潟工科大学
より
となる。
竹野茂治@新潟工科大学