3 部分積分を利用する方法
一般の 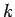 に対して
に対して 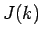 を求める方法として、
(高校などで) 最も普通に紹介される方法は、
部分積分を利用して漸化式を作る方法だと思われる。
を求める方法として、
(高校などで) 最も普通に紹介される方法は、
部分積分を利用して漸化式を作る方法だと思われる。
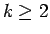 に対して部分積分を用いると、
に対して部分積分を用いると、
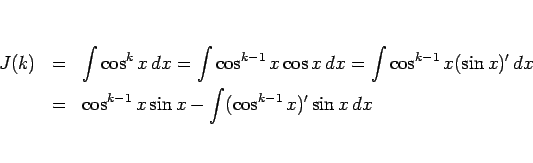
となるが、合成関数の微分により 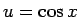 とすれば、
とすれば、
となるから、
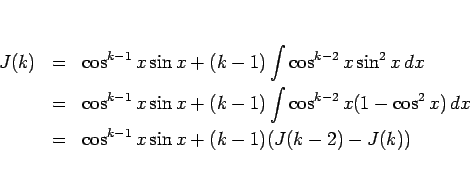
となる。よって右辺の 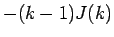 を左辺に移項すれば
を左辺に移項すれば
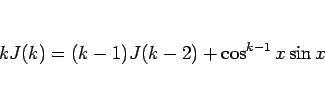
となるので、
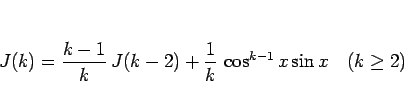 |
(9) |
が得られる。これに、
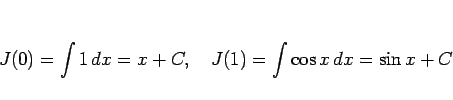 |
(10) |
を組み合わせれば、帰納的にすべての 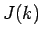 が得られることになる (奇数の
が得られることになる (奇数の 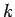 も含めて)。
も含めて)。
例えば、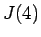 ,
,  は以下のようになる。
は以下のようになる。
2 節の最後に述べたように 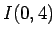 は
は 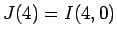 から求めることができる。
から求めることができる。
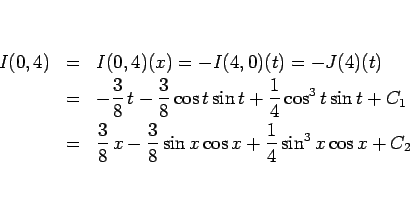
また、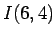 なども、途中で上の
なども、途中で上の 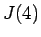 を使えば、
を使えば、
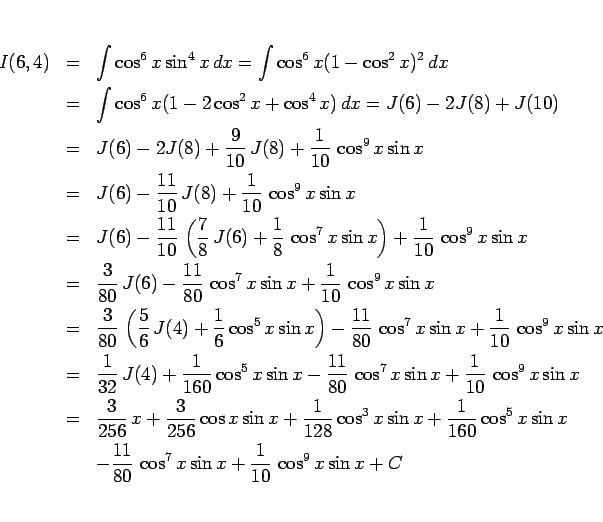
のように求められる。
この方法は、公式 (9) さえ作ってしまえば楽なのだが、
公式 (9) を作るために一旦一般の 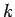 に対して部分積分を行わなければならない、
という点が難点ではないかと思われる。
に対して部分積分を行わなければならない、
という点が難点ではないかと思われる。
竹野茂治@新潟工科大学
2010年3月12日
![]() に対して部分積分を用いると、
に対して部分積分を用いると、
![]() ,
, ![]() は以下のようになる。
は以下のようになる。
![]() に対して部分積分を行わなければならない、
という点が難点ではないかと思われる。
に対して部分積分を行わなければならない、
という点が難点ではないかと思われる。