3 テイラー展開を利用する方法
2 節の方法は、考え方も計算も少し厄介である。
この節では、高校の物理で習う放物運動の式を使い、
斜面と放物運動曲線とをテイラー展開を用いて比較することで (12) を導く方法を紹介する。
今、斜面から離れていない物体の位置を 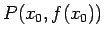 とし、
そのときの速度ベクトルを
とし、
そのときの速度ベクトルを
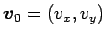 とする。
この速度ベクトルは斜面に接しているので、
その傾きと斜面の傾きは等しく、よって
とする。
この速度ベクトルは斜面に接しているので、
その傾きと斜面の傾きは等しく、よって
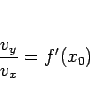 |
(13) |
が成り立つ。なお、物体は右側に移動しているので 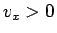 である。
である。
この 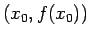 で物体が斜面から離れるかどうかを、
放物運動と比較して考えることにする。
今、仮にこの斜面がここで切れていたとすれば、
物体は
で物体が斜面から離れるかどうかを、
放物運動と比較して考えることにする。
今、仮にこの斜面がここで切れていたとすれば、
物体は 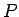 から速度
から速度
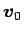 で投げた場合の放物運動をするはずである。
まずその軌跡
で投げた場合の放物運動をするはずである。
まずその軌跡 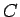 の方程式を計算しよう。
この場合、物体には鉛直下向きに
の方程式を計算しよう。
この場合、物体には鉛直下向きに 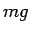 の力が働くのみなので、
その時点を時刻 0 とすれば、よく知られているように
の力が働くのみなので、
その時点を時刻 0 とすれば、よく知られているように
![\begin{displaymath}
\left\{\begin{array}{ll}
y & = \displaystyle -\frac{g}{2}t^2+v_yt+f(x_0), [.5zh]
x & = v_x t+x_0
\end{array}\right.\end{displaymath}](img62.gif) |
(14) |
が成り立つ。
これは、高校の物理でもよく用いられる式であるが、運動方程式
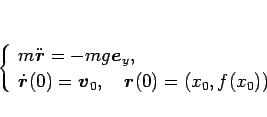
を解くことでも容易に得られる。(14) より、
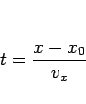
なので、これを (14) の 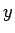 の式に代入すれば、
の式に代入すれば、
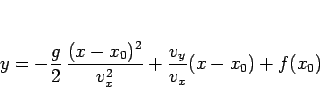
となるが、(13) よりこれは
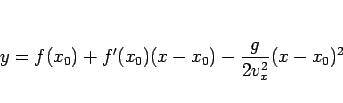 |
(15) |
と書けることになる。これが放物曲線 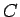 の方程式であるが、
この (15) 式は
の方程式であるが、
この (15) 式は 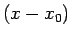 の 2 次式の形になっていることに注意する。
の 2 次式の形になっていることに注意する。
さて、もし斜面がなければ 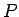 から右には物体は
この
から右には物体は
この 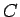 に沿って進むことになるから、
もし「
に沿って進むことになるから、
もし「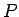 から右は斜面
から右は斜面 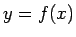 が
が 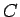 より下って」いれば、
物体は斜面から離れて
より下って」いれば、
物体は斜面から離れて 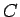 に沿った放物運動をするだろうし、
「
に沿った放物運動をするだろうし、
「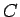 より上がって」いれば、
より上がって」いれば、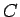 ではなく斜面に沿って動くことになる。
よって、
ではなく斜面に沿って動くことになる。
よって、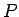 の近くで
の近くで 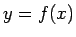 と
と 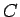 の方程式 (15) との上下関係を見ることで、
の方程式 (15) との上下関係を見ることで、
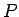 で物体が斜面から離れるかどうかがわかることになる。
で物体が斜面から離れるかどうかがわかることになる。
(15) は 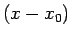 のテイラー展開の形をしているので、
のテイラー展開の形をしているので、
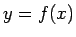 のテイラー展開
のテイラー展開
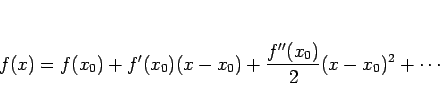 |
(16) |
と比較すれば、最初の 2 項は全く同じであることがわかる。
これは、この 2 つの曲線が 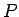 で接する (共通の接線を持つ) ことを意味する。
よって、
で接する (共通の接線を持つ) ことを意味する。
よって、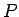 の付近での比較は
の付近での比較は 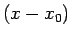 の 2 次の項を見ればよく、
そこから斜面の方が
の 2 次の項を見ればよく、
そこから斜面の方が 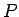 の近くで
の近くで 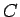 より上、すなわち離れない条件は
より上、すなわち離れない条件は
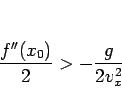 |
(17) |
であることがわかる。
一方、(13) より
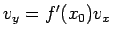 なので、速さ
なので、速さ 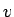 は
は
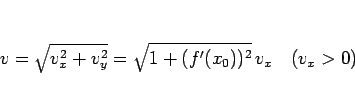
となるから、これを (17) に代入すれば、
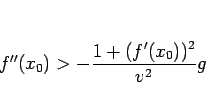 |
(18) |
となり、(12) と同じものが得られたことになる。
竹野茂治@新潟工科大学
2009年2月27日
![]() とし、
そのときの速度ベクトルを
とし、
そのときの速度ベクトルを
![]() とする。
この速度ベクトルは斜面に接しているので、
その傾きと斜面の傾きは等しく、よって
とする。
この速度ベクトルは斜面に接しているので、
その傾きと斜面の傾きは等しく、よって
![]() で物体が斜面から離れるかどうかを、
放物運動と比較して考えることにする。
今、仮にこの斜面がここで切れていたとすれば、
物体は
で物体が斜面から離れるかどうかを、
放物運動と比較して考えることにする。
今、仮にこの斜面がここで切れていたとすれば、
物体は ![]() から速度
から速度
![]() で投げた場合の放物運動をするはずである。
まずその軌跡
で投げた場合の放物運動をするはずである。
まずその軌跡 ![]() の方程式を計算しよう。
この場合、物体には鉛直下向きに
の方程式を計算しよう。
この場合、物体には鉛直下向きに ![]() の力が働くのみなので、
その時点を時刻 0 とすれば、よく知られているように
の力が働くのみなので、
その時点を時刻 0 とすれば、よく知られているように
![]() から右には物体は
この
から右には物体は
この ![]() に沿って進むことになるから、
もし「
に沿って進むことになるから、
もし「![]() から右は斜面
から右は斜面 ![]() が
が ![]() より下って」いれば、
物体は斜面から離れて
より下って」いれば、
物体は斜面から離れて ![]() に沿った放物運動をするだろうし、
「
に沿った放物運動をするだろうし、
「![]() より上がって」いれば、
より上がって」いれば、![]() ではなく斜面に沿って動くことになる。
よって、
ではなく斜面に沿って動くことになる。
よって、![]() の近くで
の近くで ![]() と
と ![]() の方程式 (15) との上下関係を見ることで、
の方程式 (15) との上下関係を見ることで、
![]() で物体が斜面から離れるかどうかがわかることになる。
で物体が斜面から離れるかどうかがわかることになる。
![]() のテイラー展開の形をしているので、
のテイラー展開の形をしているので、
![]() のテイラー展開
のテイラー展開