7 半角の公式を利用する方法
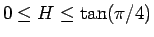 を
を
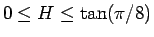 に帰着させるのに、
5 節では
に帰着させるのに、
5 節では
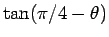 の加法定理を用いて
の加法定理を用いて
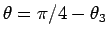 を考えたが、
その代わりに半角の公式 (9) を利用するという方法も考えられる。
を考えたが、
その代わりに半角の公式 (9) を利用するという方法も考えられる。
つまり、
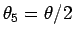 に対して、
に対して、
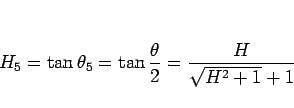
であるから、
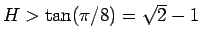 (
(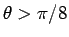 ) のときは
) のときは
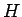 からこの式により
からこの式により 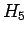 を求め、
を求め、
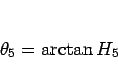
として
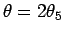 と求める方法である。
この場合も
と求める方法である。
この場合も
 となってくれるので 5 節と同等の誤差が期待できるのであるが、
しかしこの
となってくれるので 5 節と同等の誤差が期待できるのであるが、
しかしこの 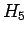 の計算には
の計算には 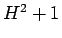 の平方根が含まれてしまう。
元の問題に戻れば、そのマイコンに任意の正の実数の平方根を計算する機能が
そなわっていない場合には、この方法が使えないことになる。
つまり、半角の公式を用いる方法はそのような目的には
ふさわしくない可能性がある。
の平方根が含まれてしまう。
元の問題に戻れば、そのマイコンに任意の正の実数の平方根を計算する機能が
そなわっていない場合には、この方法が使えないことになる。
つまり、半角の公式を用いる方法はそのような目的には
ふさわしくない可能性がある。
竹野茂治@新潟工科大学
2009年1月18日
![]() に対して、
に対して、