![$\displaystyle A=\frac{1}{7}\left[\begin{array}{ccc}{2}&{-3}&{-6}\\
{3}&{6}&{-2}\\
{6}&{-2}&{3}\end{array}\right]
$](img358.png)
![$\displaystyle A=\frac{1}{7}\left[\begin{array}{ccc}{2}&{-3}&{-6}\\
{3}&{6}&{-2}\\
{6}&{-2}&{3}\end{array}\right]
$](img358.png)
![\begin{eqnarray*}49A\,{}^T\!{A}
&=&
\left[\begin{array}{ccc}{2}&{-3}&{-6}\\
...
...2-6}\\
{12+6-18}&{18-12-6}&{36+4+9}\end{array}\right]
\ =\ 49E\end{eqnarray*}](img359.png)
 は直交行列。
は直交行列。
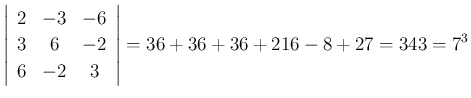
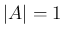 となるので、回転変換の行列になっている。
となるので、回転変換の行列になっている。
![$\displaystyle A-E=\frac{1}{7}\left[\begin{array}{ccc}{-5}&{-3}&{-6}\\
{3}&{-1}&{-2}\\
{6}&{-2}&{-4}\end{array}\right]
$](img361.png)
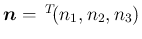 は、
は、
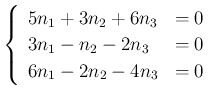
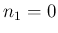 ,
, 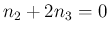 、よって
と取れる。次は、回転角
、よって
と取れる。次は、回転角 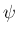 を計算する。
を計算する。
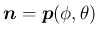 とすると、
とすると、
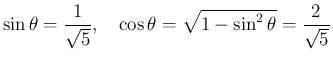
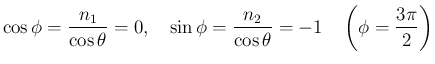
![$\displaystyle \mbox{\boldmath$\hat{n}$}
= \left[\begin{array}{c}{\cos\phi\sin\...
...=\left[\begin{array}{c}{1}\\ {0}\\ {0}\end{array}\right] = \mbox{\boldmath$i$}
$](img368.png)
![$\displaystyle A\mbox{\boldmath$\hat{n}$}
= \frac{1}{7\sqrt{5}}\left[\begin{arr...
...\left[\begin{array}{c}{2}\\ {3}\\ {6}\end{array}\right]=\mbox{\boldmath$\ell$}
$](img369.png)
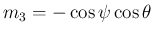 ,
,
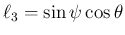 より
となる。よって、(52) が回転軸 (
より
となる。よって、(52) が回転軸 (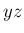 平面内)、
(53) の
平面内)、
(53) の 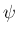 (
(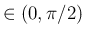 ) が
回転角となる回転変換を表すことになる。
) が
回転角となる回転変換を表すことになる。
次に、この回転を、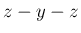 の軸回転
の軸回転
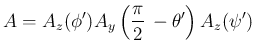
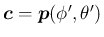 とすれば
とすれば
![$\displaystyle \frac{1}{7}\left[\begin{array}{c}{-6}\\ {-2}\\ {3}\end{array}\rig...
...os\phi'\cos\theta'}\\ {\sin\phi'\cos\theta'}\\ {\sin\theta'}\end{array}\right]
$](img378.png)
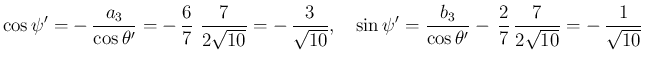
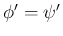 (
(
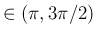 ) となる。
) となる。
なお、
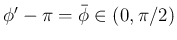 とすると、
とすると、
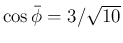 より、
より、
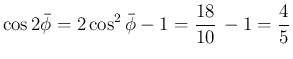
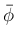 は、3:4:5 の直角三角形の最小角の半分になる。
は、3:4:5 の直角三角形の最小角の半分になる。
竹野茂治@新潟工科大学