2 逆行列
行列 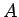 の逆行列
の逆行列 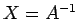 は、
は、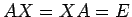 となるものを言うが、
実際には
となるものを言うが、
実際には 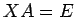 さえ成り立てば、
さえ成り立てば、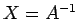 となる。
となる。
今、3 次の正方行列 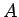 を列ベクトルに、
を列ベクトルに、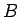 を行ベクトルに分けて、
を行ベクトルに分けて、
![\begin{displaymath}
A=\left[\mbox{\boldmath$a$}_1\ \mbox{\boldmath$a$}_2\ \mbox{...
...boldmath$b$}_2\\ {}^t\!\mbox{\boldmath$b$}_3\end{array}\right]
\end{displaymath}](img11.gif)
(
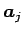 ,
,
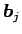 はいずれも列ベクトル) として積
はいずれも列ベクトル) として積 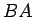 を考えると、
を考えると、
![\begin{eqnarray*}BA
&=&
\left[\begin{array}{c}{}^t\!\mbox{\boldmath$b$}_1\\ {...
...& (\mbox{\boldmath$b$}_3,\mbox{\boldmath$a$}_3)\end{array}\right]\end{eqnarray*}](img15.gif)
となることがわかる。
ここで、
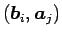 はベクトル
はベクトル
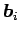 と
と
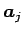 の内積で、行列としての積
の内積で、行列としての積
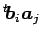 は明らかに、
ベクトルとしての内積
は明らかに、
ベクトルとしての内積
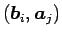 に等しい。
に等しい。
もし、この 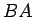 が対角行列になるとすると、
が対角行列になるとすると、
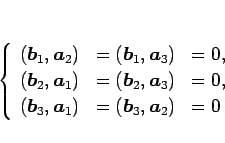
でなければならないが、これは、
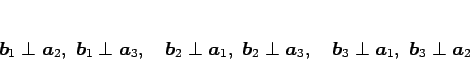
を意味する。
よって、例えば
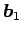 は
は
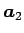 ,
,
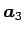 に垂直であるから、
その外積
に垂直であるから、
その外積
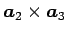 に平行であることになり、同様にして、
に平行であることになり、同様にして、
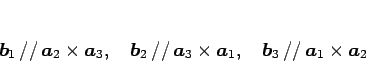
が成り立つことになる。
そして、今
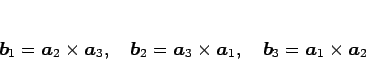 |
(3) |
とすると、
ベクトル
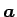 ,
,
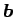 ,
,
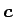 の三重積
の三重積
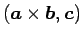 が、
が、
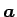 ,
,
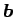 ,
,
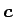 の作る行列の行列式に等しい (教科書 [1] p58 (14.6)) という性質:
の作る行列の行列式に等しい (教科書 [1] p58 (14.6)) という性質:
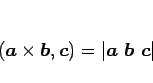
および定理 15.4 により、
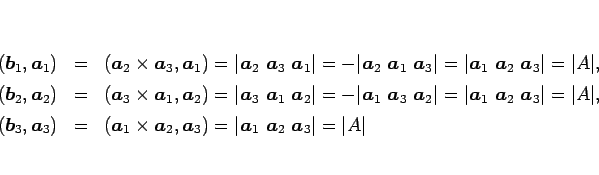
となるので、この (3) による 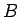 、すなわち
、すなわち
![\begin{displaymath}
B = {}^t\!\left[\mbox{\boldmath$a$}_2\times\mbox{\boldmath$...
..._1
\ \ \mbox{\boldmath$a$}_1\times\mbox{\boldmath$a$}_2\right]\end{displaymath}](img33.gif) |
(4) |
に対して、
![\begin{displaymath}
BA = \left[\begin{array}{ccc}\vert A\vert&0&0\\ 0&\vert A\vert&0\\ 0&0&\vert A\vert\end{array}\right] = \vert A\vert E
\end{displaymath}](img34.gif)
が成り立つことになる。よって (2) により、
この 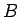 は
は 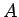 の余因子行列
の余因子行列 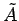 に等しいことがわかる。
に等しいことがわかる。
結局、3 次の逆行列を求める場合、
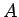 の列ベクトルの外積からなる行列の転置行列 (4) を計算すれば
これが余因子行列となるので、
これを
の列ベクトルの外積からなる行列の転置行列 (4) を計算すれば
これが余因子行列となるので、
これを 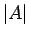 で割れば
で割れば 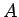 の逆行列が求まることがわかったことになる。
の逆行列が求まることがわかったことになる。
竹野茂治@新潟工科大学
2010年7月9日
![]() を列ベクトルに、
を列ベクトルに、![]() を行ベクトルに分けて、
を行ベクトルに分けて、
![]() が対角行列になるとすると、
が対角行列になるとすると、
![]() の列ベクトルの外積からなる行列の転置行列 (4) を計算すれば
これが余因子行列となるので、
これを
の列ベクトルの外積からなる行列の転置行列 (4) を計算すれば
これが余因子行列となるので、
これを ![]() で割れば
で割れば ![]() の逆行列が求まることがわかったことになる。
の逆行列が求まることがわかったことになる。