3 外積の大きさ
まずは、外積の大きさに関して、
(1) から 1. を示すことを考えるが、
これは単純に成分計算で示すことができる。
今、
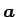 と
と
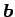 のなす角を
のなす角を 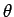 (
(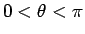 ) とする。
) とする。
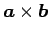 の長さの 2 乗を考えると、
の長さの 2 乗を考えると、
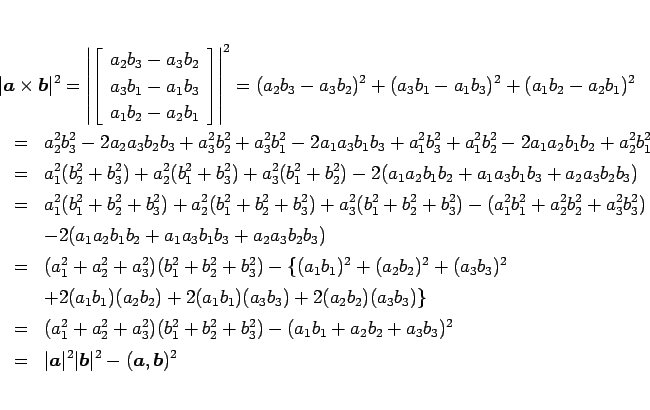
となる。ここで、
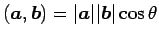 なので、
なので、
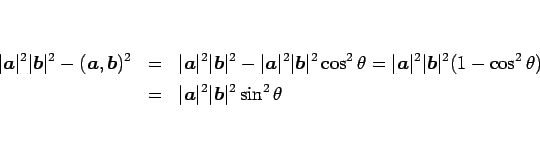
となる。よって、結局
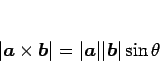 |
(2) |
となることがわかる。
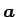 ,
,
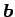 が作る平行四辺形を考えると、
が作る平行四辺形を考えると、
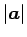 を底辺と見れば、
を底辺と見れば、
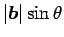 がそれに垂直な高さになるので、
よって (2) の右辺は、
がそれに垂直な高さになるので、
よって (2) の右辺は、
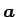 ,
,
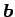 が作る平行四辺形の面積に等しくなる。
が作る平行四辺形の面積に等しくなる。
竹野茂治@新潟工科大学
2009年5月26日
![]() と
と
![]() のなす角を
のなす角を ![]() (
(![]() ) とする。
) とする。
![]() の長さの 2 乗を考えると、
の長さの 2 乗を考えると、