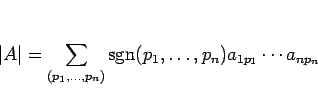
具体的な行列式の実際の計算には、 順列の符号の式を用いることはなく、 この帰納的な定義の方が計算向きであるし、式もわかりやすく、 順列の符号を説明する必要もないのでそのようにしているのであるが、 色んな行列式の性質を証明するには順列の符号による定義の方が有利である。
逆に言えば、帰納的な定義からでは、 教科書に載っている性質の証明は割と面倒になる。 ここでは、その帰納的な定義による行列式の性質の証明を考察してみる。
なおこのような話題は、学生にとっておもしろいものや 意味のあるものではなく、むしろ数学者等にしか興味のない話であろうことを 最初に断っておく。
竹野茂治@新潟工科大学