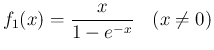
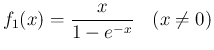
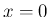 では分母は 0 になってしまうが、分子もそこで 0 なので、
では分母は 0 になってしまうが、分子もそこで 0 なので、
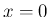 では 0/0 の不定形になっていて、
では 0/0 の不定形になっていて、
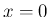 への極限値は 1 となることが容易にわかる。
関数論の言葉を使えば、この
への極限値は 1 となることが容易にわかる。
関数論の言葉を使えば、この 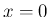 は
は 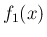 の
除去可能特異点になっていて、よって、
の
除去可能特異点になっていて、よって、
![$\displaystyle f_1(x) =
\left\{\begin{array}{ll}
\displaystyle \frac{x}{1-e^{-x}} & (x\neq 0)\ [1zh]
1 & (x=0)\end{array}\right.$](img5.png)
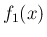 は滑らかな関数、特に解析関数になり、
当然マクローリン展開も可能である。
そのマクローリン展開の方法を紹介する。
は滑らかな関数、特に解析関数になり、
当然マクローリン展開も可能である。
そのマクローリン展開の方法を紹介する。
一般に、 の
の 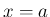 でのテイラー展開が、
でのテイラー展開が、
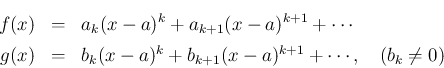
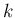 位 (
位 (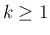 ) の零点を持つ場合、
商
) の零点を持つ場合、
商 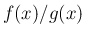 は 0/0 となるが、
は 0/0 となるが、 で約分ができるため
で約分ができるため 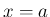 での
極限は存在し、
での
極限は存在し、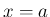 はこの商の除去可能特異点となる。よってこの商を
はこの商の除去可能特異点となる。よってこの商を
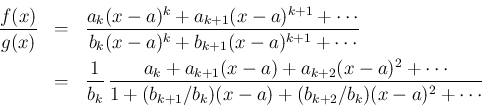
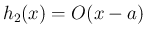 であるから、分母は
のように展開ができることになる。
この式に、(1), (2) を代入して形式的に展開すれば、
であるから、分母は
のように展開ができることになる。
この式に、(1), (2) を代入して形式的に展開すれば、
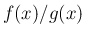 の
の 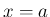 でのテイラー展開が得られることになる。
例えば、3 次以上の項を
でのテイラー展開が得られることになる。
例えば、3 次以上の項を 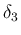 と書くことにして 2 次の項まで
計算すれば、
と書くことにして 2 次の項まで
計算すれば、
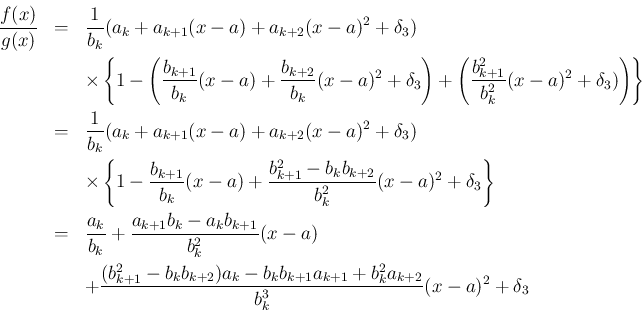
これと同じようにすれば、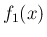 のマクローリン展開も得られ、
のマクローリン展開も得られ、
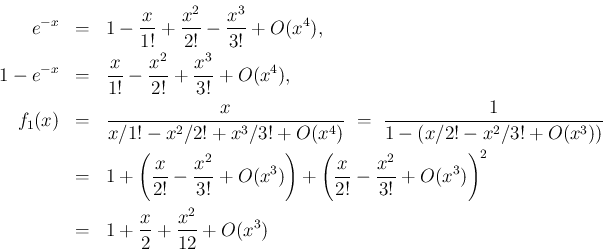
つまり、0/0 の場合は、テイラー展開レベルで約分をし、 それから商のテイラー展開の手法を利用すればいいわけである。
なお、元の質問者は、
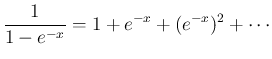
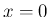 の近くでは
の近くでは 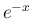 は 0 に近くない (1 に近い) ため
このような展開はできない。
は 0 に近くない (1 に近い) ため
このような展開はできない。
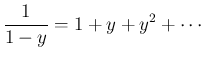
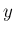 が 0 に近い場合 (正確には
が 0 に近い場合 (正確には 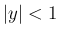 の
場合) だけである。
このように、合成関数の形でテイラー展開を行う場合には、
そういう点に注意する必要がある。
の
場合) だけである。
このように、合成関数の形でテイラー展開を行う場合には、
そういう点に注意する必要がある。
竹野茂治@新潟工科大学