2 指数関数
まずは、指数関数の導関数の公式
から考える。
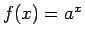 (
(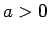 ,
, 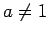 ) とすると、
) とすると、
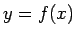 のグラフの
のグラフの 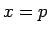 での傾きは
での傾きは 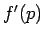 である。
である。
今
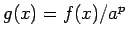 とすると、
とすると、
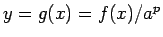 のグラフは
のグラフは 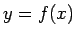 のグラフを
のグラフを 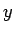 方向に
方向に 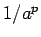 倍したものだから
倍したものだから 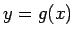 の
の 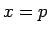 での傾き
での傾き 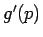 は
は
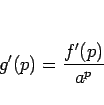 |
(4) |
となる。一方、指数関数の性質により、
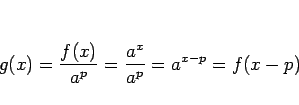 |
(5) |
であるから、
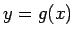 は
は 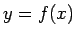 を
を 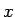 方向に
方向に 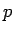 だけ平行移動したものとなり、
だけ平行移動したものとなり、
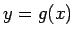 の
の 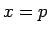 でのグラフの傾き
でのグラフの傾き 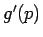 は、
は、
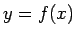 の
の 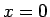 でのグラフの傾き
でのグラフの傾き 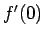 に等しいことになる (図 1)。
に等しいことになる (図 1)。
図 1:
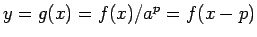 のグラフと傾き
のグラフと傾き
|
|
よって、(4) と 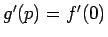 により
により
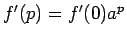 がわかり、
がわかり、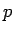 は任意なので、
は任意なので、
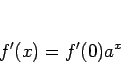 |
(6) |
が得られる。あとは 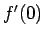 の値を決定すればよい。
の値を決定すればよい。
この 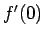 の値は
の値は 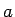 によって変わるが、
によって変わるが、
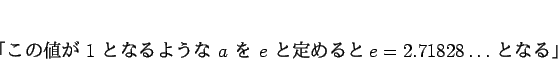 |
(7) |
という形で 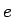 を定義すれば、
(6) から (2) が得られることになる。
を定義すれば、
(6) から (2) が得られることになる。
この (7) は、高校の教科書での通常の 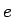 の定義
の定義
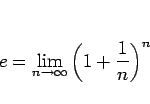 |
(8) |
とは異なるが、(7) は極限で書けば
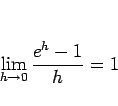 |
(9) |
となり、これは 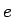 のみが持つ性質であるから、
(7) による定義でも (8) と
同じものが得られることが保証される。
ちなみに、(7) のような
のみが持つ性質であるから、
(7) による定義でも (8) と
同じものが得られることが保証される。
ちなみに、(7) のような 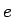 の定義の仕方は、
現在私が使用している教科書 [1] でも採用している方法である。
の定義の仕方は、
現在私が使用している教科書 [1] でも採用している方法である。
一般の 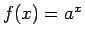 の場合は、
の場合は、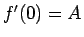 とすると、
とすると、
より 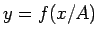 も指数関数であり、そのグラフは
も指数関数であり、そのグラフは 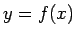 のグラフを
のグラフを 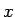 方向に
方向に 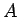 倍したものなので、
倍したものなので、
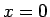 での傾きは
での傾きは 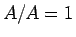 になり、
よって (7) により
になり、
よって (7) により 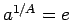 であることがわかる。
よって、
であることがわかる。
よって、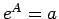 より
より
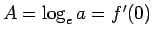 となるので、
これを (6) に代入すれば (3) が
得られる。
となるので、
これを (6) に代入すれば (3) が
得られる。
竹野茂治@新潟工科大学
2017年4月11日
![]() (
(![]() ,
, ![]() ) とすると、
) とすると、
![]() のグラフの
のグラフの ![]() での傾きは
での傾きは ![]() である。
である。
![]() とすると、
とすると、
![]() のグラフは
のグラフは ![]() のグラフを
のグラフを ![]() 方向に
方向に ![]() 倍したものだから
倍したものだから ![]() の
の ![]() での傾き
での傾き ![]() は
は
![]() により
により
![]() がわかり、
がわかり、![]() は任意なので、
は任意なので、
![]() の値は
の値は ![]() によって変わるが、
によって変わるが、
![]() の定義
の定義
![]() の場合は、
の場合は、![]() とすると、
とすると、