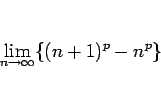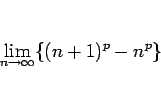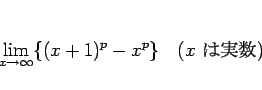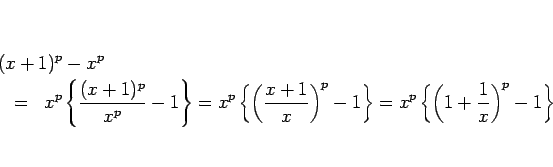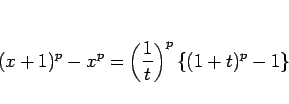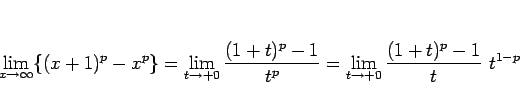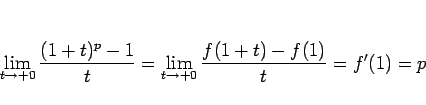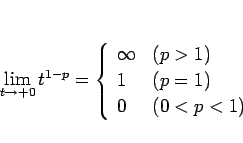次へ: 3 おわりに
上へ: 巾乗の差の極限について
前へ: 1 はじめに
(PDF ファイル: infdiff.pdf)
2 考察
数列の極限
は、もし実数の極限
が存在すれば、もちろんそれと同じ極限を持つはずなので、
こちらを考えることにします。
となるので、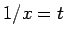 とおくと、この式は
とおくと、この式は
となります。
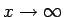 と
と
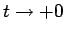 は同じことですから、
よって、
は同じことですから、
よって、
となりますが、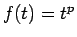 とすれば
とすれば
(
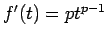 ) となることがわかります。
) となることがわかります。
一方、
なので、結局、
であることが言えることになります。
次へ: 3 おわりに
上へ: 巾乗の差の極限について
前へ: 1 はじめに
竹野茂治@新潟工科大学
2006年4月25日