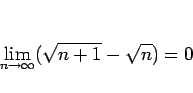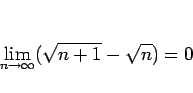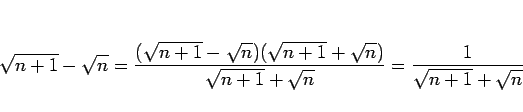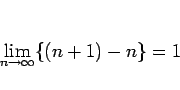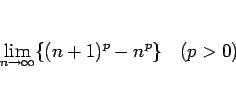次へ: 2 考察
上へ: 巾乗の差の極限について
前へ: 巾乗の差の極限について
(PDF ファイル: infdiff.pdf)
1 はじめに
極限のところで、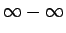 の不定形の例として、
の不定形の例として、
であること (正確に言えば、これとほぼ同等の問題) を、
を利用して示しました。
その一方で、
となります。では、一般に、
の極限はどうなるのでしょうか。
講義の寄り道として、少し考えてみましょう。
次へ: 2 考察
上へ: 巾乗の差の極限について
前へ: 巾乗の差の極限について
竹野茂治@新潟工科大学
2006年4月25日