1 はじめに
以前、高校の数学教員から、高校の数学では指数を拡張して
指数関数 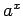 を考えるが、
を考えるが、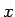 が有理数まではちゃんと定義するものの
実数への拡張は適当に流している、もう少しちゃんと定義できないか、
という質問を受けたことがある。
が有理数まではちゃんと定義するものの
実数への拡張は適当に流している、もう少しちゃんと定義できないか、
という質問を受けたことがある。
確かに「無理数乗」をちゃんと定義することは容易ではなく、
通常高校の教科書でさらっと触れている「有理数乗の極限」による定義も、
以下にあるようにそれなりの準備が必要となる。
- 多少の実数論といくつかの定理 (極限の存在の保証のため)
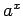 の、有理数の
の、有理数の 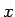 に対する定義とそれに対する指数法則の証明
に対する定義とそれに対する指数法則の証明
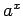 の、有理数の
の、有理数の 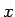 に関する単調性とある種の連続性
に関する単調性とある種の連続性
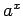 の、無理数の
の、無理数の 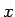 に関する定義 (がちゃんと定義されること)
に関する定義 (がちゃんと定義されること)
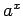 の、無理数を含む実数の
の、無理数を含む実数の 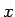 に対する指数法則の証明
に対する指数法則の証明
この方向での実数乗の詳しい説明は、
例えば [1] の第 3 章 §3 に書かれているが、
そこでは上限 (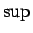 )、下限 (
)、下限 (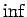 ) を使っているので、
その前にある程度の実数論と上限、下限に関する議論などが必要となる。
) を使っているので、
その前にある程度の実数論と上限、下限に関する議論などが必要となる。
一方で、オイラーも指摘している ([3] 13 節、
または [4] 5.4 節) ように、
指数関数「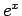 」は有理数乗の極限を用いなくても、
自然数乗と極限だけで以下の式によって得られる。
」は有理数乗の極限を用いなくても、
自然数乗と極限だけで以下の式によって得られる。
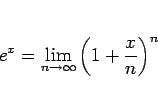 |
(1) |
これを 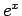 の定義として考えれば有理数乗の極限によらずに
の定義として考えれば有理数乗の極限によらずに 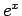 が得られ、
その逆関数により自然対数
が得られ、
その逆関数により自然対数 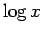 (
(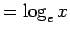 ) を定義すれば、
一般の正の実数
) を定義すれば、
一般の正の実数 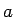 (
(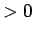 ) の
) の 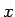 乗も、
乗も、
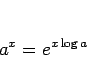 |
(2) |
により、有理数乗の極限を使わずに得られる。
そしてこの方向なら、累乗は自然数乗しか使わないので、
負の整数乗や有理数乗などの拡張をせずに、
実数乗をすべてこの式で定義してしまうことすら可能である。
本稿では、このような方向で指数関数を定義する場合、
その性質等の証明等を紹介する。
上で述べたように、本稿では負の整数乗、有理数乗すら仮定せず、
そして使わずに、通常のそれらと同等のもの、
および指数法則、指数関数の性質が成り立つことなどを考察する。
最後に、さらなる発展として複素数乗についても考察する。
なお、本稿では、ほぼ高校程度 (数学 I,II,III) の数学の知識のみを
仮定して話をするが、それを越える理論、議論が必要となる部分では、
そこで必要となる知識を紹介し、それを認めて話を進めることとする。
竹野茂治@新潟工科大学
2017年2月2日
![]() 」は有理数乗の極限を用いなくても、
自然数乗と極限だけで以下の式によって得られる。
」は有理数乗の極限を用いなくても、
自然数乗と極限だけで以下の式によって得られる。