F(s) = 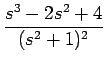
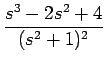
例えば、
の場合を考える。定理 2 により、
F(s) =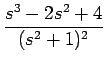
とおくことができる。 ただし、この場合定数 a, b, c, d は複素数であることに注意する。 (9) の右辺を通分すると、その分子は、
F(s) = =
+
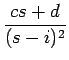
(9)
| (as+b)(s-i)2+(cs+d )(s+i)2 | |||
| = | (as + b)(s2 -2si - 1) + (cs + d )(s2 + 2si - 1) | ||
| = | as3 + (- 2ai + b)s2 + (- a - 2bi)s - b | ||
| + cs3 + (2ci + d )s2 + (- c + 2di)s - d | |||
という連立方程式を得る。これを解いて a, b, c, d を求めればよいが、 2 本目、3 本目の式を
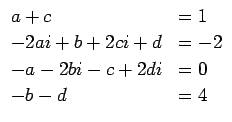
(10)
と変形すれば、1 本目、4 本目の式より
-2i(a - c) + (b + d )= - 2, - (a + c) - 2i(b - d )= 0
となるので、
-2i(a - c) = 2, - 2i(b - d )= 1
となる。これと 1 本目、4 本目の式を組み合わせれば、結局
a - c = i, b - d =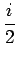
が得られる。
a =+
, b = - 2 +
, c =
-
, d = - 2 -
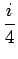
なお、この結果を見ると c = ![]() , d =
, d = ![]() であることがわかるが、
これは実は (9) から導くこともできる。
F(s)
は元々実数係数の有理関数なので、
(9) の共役を考えれば、共役の性質
であることがわかるが、
これは実は (9) から導くこともできる。
F(s)
は元々実数係数の有理関数なので、
(9) の共役を考えれば、共役の性質
を用いることにより以下のようになる:
=
+
,
=
-
,
=
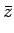
,
=
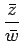
これも F(s) の部分分数分解であり、この係数は一意に決まるので、 (9) と比較すれば、
= F(s) =
=
+
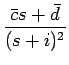
となり、よって c =
s +
= cs + d,
s +
= as + b
となることになる。最後の分数式は
F(s) =+
=
+
= 2
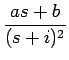
となるので、元の式と比較すれば、
=
=
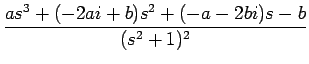
となるが、
{as3 + (- 2ai + b)s2 + (- a - 2bi)s - b} =
- s2 + 2
となるので、よって、
a =
, 2
a +
b = - 1, -
a + 2
b = 0, -
b = 2
つまり
a =
,
a =
,
b = - 2,
b =
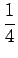
と得られる。 こちらの方が (10) に比べて 多少は式の処理はやさしく見えなくもない。
a =+
, b = - 2 +
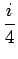
しかし、いずれにせよ、この方法では分母の次数が大きい場合、 例えば (s2 +1)5 のような場合は、計算量が非常に多く、 あまり易しい計算方法ではない。
竹野茂治@新潟工科大学