F(s) = 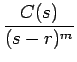 (deg C = l < m)
(deg C = l < m)
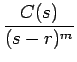 (deg C = l < m)
(deg C = l < m)
の場合を考える。s - r = S とすれば s = S + r より、
F(s) =(deg C = l < m)
のように書ける。 ここで、
F(s) ==
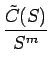
と書くことにすれば、
(S) = a0 + a1S + ... + alSl
と変形できるので、
F(s) ==
+
+ ... +
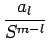
| F(s) | = | a0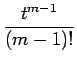 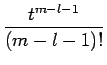 |
|
| = | 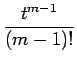 + ... + al + ... + al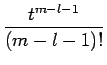 |
||
| = | 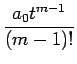 + ... + + ... + 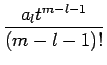 |
が得られる。
-1[F(s)] = ert
+ ... +
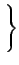
例えば、
の場合を考えると、S = s + 2 とすれば、
F(s) =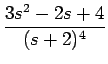
| F(s) | = | 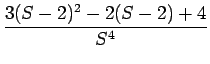 = = 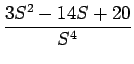 = = |
|
| = | 3 |
||
| = | |||
| = |
となるわけである。
-1[F] = e-2t
3t - 7t2 +
t3
竹野茂治@新潟工科大学