

Next: 3 周期解の個数
Up: 単独保存則方程式の周期解の数値解析 II
Previous: 1 はじめに
(PDF ファイル: kiyou2003.pdf)
2 粘性方程式の周期解
本稿や前回の報告[4]では,保存則方程式の数値計算では
段階的な Lax-Friedrichs 法と呼ばれる以下の差分法を用いている.
この差分法は,
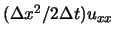 の形の誤差を持ち,よって
以下の形の粘性保存則方程式の解に似た性質を持つ.
の形の誤差を持ち,よって
以下の形の粘性保存則方程式の解に似た性質を持つ.
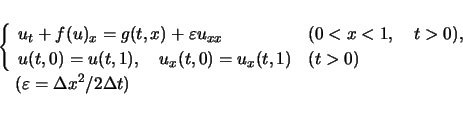 |
(2) |
ここで,比
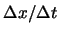 は CFL 条件によりほぼ一定に固定し,よって
は CFL 条件によりほぼ一定に固定し,よって
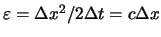 と考えることができるので,
と考えることができるので,
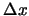 がある程度小さくないと数値計算結果に粘性効果による影響が現われる.
がある程度小さくないと数値計算結果に粘性効果による影響が現われる.
前回の報告[4]においても 4,5 節において
その粘性効果の影響について実験,考察し,
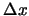 が小さい場合,すなわち粘性効果が小さい方が倍周期性が
はっきり現われるという数値計算結果を紹介し,
逆に粘性効果は倍周期性を消す方向に働くのではないか,と予想しているが,
その後,倍周期性と粘性効果の関係を進行波解
が小さい場合,すなわち粘性効果が小さい方が倍周期性が
はっきり現われるという数値計算結果を紹介し,
逆に粘性効果は倍周期性を消す方向に働くのではないか,と予想しているが,
その後,倍周期性と粘性効果の関係を進行波解
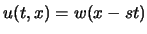 (
(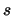 は定数)
に関して数学的に考察することで,次の結果を得た.
は定数)
に関して数学的に考察することで,次の結果を得た.
定理 1
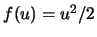 の非粘性 Burgers 方程式 (1)
では,任意の整数
の非粘性 Burgers 方程式 (1)
では,任意の整数 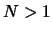 に対し,外力の周期の
に対し,外力の周期の 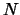 倍の周期を持つ
進行波型
倍の周期を持つ
進行波型
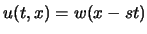 の周期解と
の周期解と 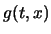 の例を構成できる.
の例を構成できる.
定理 2
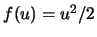 の粘性 Burgers 方程式 (2)
では,
の粘性 Burgers 方程式 (2)
では,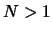 に対して,外力の周期の
に対して,外力の周期の 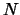 倍の周期を持つ
進行波型
倍の周期を持つ
進行波型
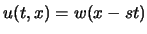 の周期解は存在しない.
の周期解は存在しない.
これらはあくまで進行波解に制限した形の結果であるが,
粘性のついた方程式ではその粘性効果によって倍周期性が起こらず,
倍周期性は非粘性方程式に特別な性質であることが分かる.
次に,粘性以外の効果が働いた場合として,さらに高次導関数項がついた方程式
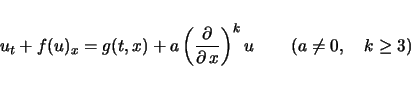 |
(3) |
ではどうなるかを考察してみた.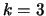 の場合の高次付加項は
特に分散項と呼ばれ,いわゆる KdV 方程式と同等である.
この場合も進行波解に関しては次の結果が得られた.
の場合の高次付加項は
特に分散項と呼ばれ,いわゆる KdV 方程式と同等である.
この場合も進行波解に関しては次の結果が得られた.
定理 3
方程式 (3) では,外力の周期の 2 倍の周期を持つ
進行波型の周期解と 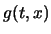 の例を構成できる.
の例を構成できる.
高次の項がついた場合は,粘性の場合とは異なり倍周期性を持ち得ることになり,
よって,その倍周期性を消すのは粘性効果のみであることが,
進行波解に関しては示されたことになる.
ただし,進行波解とは限らない一般の周期解に対して,
粘性方程式が倍周期性を持たないことはまだ証明されてはおらず,
現在のところまだ未解決である.


Next: 3 周期解の個数
Up: 単独保存則方程式の周期解の数値解析 II
Previous: 1 はじめに
Shigeharu TAKENO
2003年 11月 6日
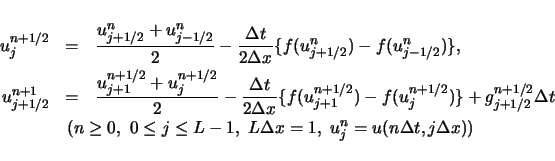
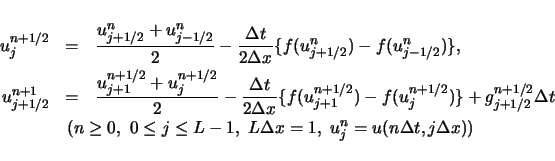
![]() が小さい場合,すなわち粘性効果が小さい方が倍周期性が
はっきり現われるという数値計算結果を紹介し,
逆に粘性効果は倍周期性を消す方向に働くのではないか,と予想しているが,
その後,倍周期性と粘性効果の関係を進行波解
が小さい場合,すなわち粘性効果が小さい方が倍周期性が
はっきり現われるという数値計算結果を紹介し,
逆に粘性効果は倍周期性を消す方向に働くのではないか,と予想しているが,
その後,倍周期性と粘性効果の関係を進行波解
![]() (
(![]() は定数)
に関して数学的に考察することで,次の結果を得た.
は定数)
に関して数学的に考察することで,次の結果を得た.