(PDF ファイル: kiyou2003.pdf)

1 はじめに

以前報告[4]したように， 時間周期的な外力を含む単独の保存則方程式の境界値問題

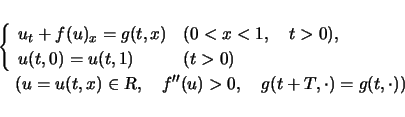$$\begin{array}{l} \left\{\begin{array}{ll} u_t + f(u)_x = ... ...1em}f''(u)>0,\hspace*{1em}g(t+T,\cdot)=g(t,\cdot)) \end{array}$$ (1)

の周期解の様相は単純ではなく，解明されていない多くの現象を引き起こす． 例えば周期解の一意性が保証されず，外力の周期の 2 倍，3 倍の周期を持つ 周期解が存在することが，それら多くの問題を引き起こしていると考えられる．

初期平均値を

$$\bar{u} = \int_0^1 u(0,x)dx$$

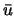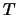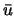とすると，外力項がある種の条件を満たす場合に， $\bar {u}$ の任意の値に対し外力と同じ周期 ($T$) を持つ周期解が 少なくとも一つ存在することが知られている[1]が， 前回の報告[4]で見たように， 適当な初期値からスタートした解の漸近的な収束先として得られる， ある意味で安定な周期解は必ずしも外力とは同周期ではなく， 外力の 2 倍，3 倍などの周期を持ち得る． その場合でも外力と同周期の解の存在は保証されるので， 周期解は外力と $\bar {u}$ に関して一意的には決定しないことになる．

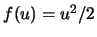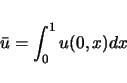
本報告では，Burgers 方程式 ($f(u)=u^2/2$) に対して， 前回の報告[4]で得られた事実や予想などに関して， その後に行なった解析や数値計算によってわかってきた周期解の性質， 特に倍周期解の存在や非存在と粘性との関係， 周期解の集合の構造などについて述べる．