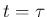 で、
それに関係するいくつかの front の速度を変更して、
その衝突時刻をずらす場合、その時刻が小さくなるように
ずらしてしまうと、現時点からそこに戻らないといけないので、
先の方に近似解を延長できる保証を与えるのが難しいので、
当然ずらす場合は衝突時刻を今より後の方にずらす方がよい。
で、
それに関係するいくつかの front の速度を変更して、
その衝突時刻をずらす場合、その時刻が小さくなるように
ずらしてしまうと、現時点からそこに戻らないといけないので、
先の方に近似解を延長できる保証を与えるのが難しいので、
当然ずらす場合は衝突時刻を今より後の方にずらす方がよい。
まず、速度の変更は本稿では「右から」そして「速度を増やす」方向で 考えることにする。その理由を以下に説明する。
ある衝突時刻 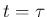 で、
それに関係するいくつかの front の速度を変更して、
その衝突時刻をずらす場合、その時刻が小さくなるように
ずらしてしまうと、現時点からそこに戻らないといけないので、
先の方に近似解を延長できる保証を与えるのが難しいので、
当然ずらす場合は衝突時刻を今より後の方にずらす方がよい。
で、
それに関係するいくつかの front の速度を変更して、
その衝突時刻をずらす場合、その時刻が小さくなるように
ずらしてしまうと、現時点からそこに戻らないといけないので、
先の方に近似解を延長できる保証を与えるのが難しいので、
当然ずらす場合は衝突時刻を今より後の方にずらす方がよい。
そして衝突時刻を後の方にずらすためには、左の front の速度を遅くするか、 または右の front の速度を速くするかの いずれかである (図 3)。
しかし、左の front は非物理 front である可能性もあり、 (T3) からそれは変更できないので、 その場合はそれより右の速度を上げざるを得なくなる。 衝突の際の右の front が非物理 front であることはないので、 よって、最初から右の front の速度を上げる、 という方向で考えればよい。
さて、!(T1) がある衝突点
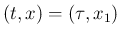 で起きている場合、
それは、そこで衝突している
で起きている場合、
それは、そこで衝突している 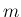 個の front (
個の front (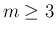 ) を
右の方から 2 つずつを組にして、少しずつ速度を上げることで、
) を
右の方から 2 つずつを組にして、少しずつ速度を上げることで、
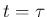 のままとし、
のままとし、
front の総数は有限なので、
まず、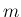 個の front のうち一番右のものの速度を少し上げて、
それが
個の front のうち一番右のものの速度を少し上げて、
それが
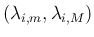 の範囲で、
かつ定義 7.1 の条件を満たし、
かつ他の front とは
の範囲で、
かつ定義 7.1 の条件を満たし、
かつ他の front とは 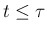 では新たにぶつからないように
できることは明らかである。
その
では新たにぶつからないように
できることは明らかである。
その 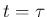 での位置を
での位置を 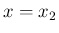 とする (
とする (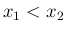 )。
なお、この front は
)。
なお、この front は 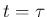 では
では 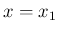 から
から 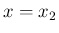 までは
速度を変更することができる。
までは
速度を変更することができる。
次に、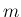 個の右から 2 番目の front の速度を
同様の条件を満たしながら上げるが、
それが 1 つ目の front と
個の右から 2 番目の front の速度を
同様の条件を満たしながら上げるが、
それが 1 つ目の front と
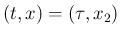 で
衝突するところまで上げられることは保証できない。
それは、
で
衝突するところまで上げられることは保証できない。
それは、
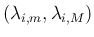 の範囲の条件や
定義 7.1 の条件を越える可能性もあるし、
または
の範囲の条件や
定義 7.1 の条件を越える可能性もあるし、
または 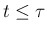 で他の front と衝突する可能性もあるからである。
で他の front と衝突する可能性もあるからである。
しかし条件内で右から 2 つ目の front の速度を少しだけ
上げることは可能なので、その 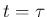 での場所を
での場所を 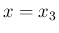 とする。
このとき、
とする。
このとき、
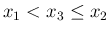 であり、
よって最初の front を
であり、
よって最初の front を 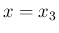 まで戻せば、
丁度
まで戻せば、
丁度
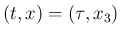 でこの 2 つの front が衝突する。
このようにして、一番右の 2 つの front を条件を満たしながら
少しだけ速度を上げて
でこの 2 つの front が衝突する。
このようにして、一番右の 2 つの front を条件を満たしながら
少しだけ速度を上げて 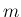 個の front から分離できることが
わかる (図 5)。
個の front から分離できることが
わかる (図 5)。
後は帰納的にこれを行えば、
最終的には !(T1) が ![$[m/2]$](img624.png) 個の !(T2) の状態に還元されることになる。
この操作では、膨張 front や接触不連続 front も速度を変更する
可能性はあるが、
他の front との衝突を新たに作ってはいないので、
操作前の !(T1) の状態で !(T4) が起きていなければ、
それを上のように分解した !(T2) にも !(T4) は起きていないはずである。
個の !(T2) の状態に還元されることになる。
この操作では、膨張 front や接触不連続 front も速度を変更する
可能性はあるが、
他の front との衝突を新たに作ってはいないので、
操作前の !(T1) の状態で !(T4) が起きていなければ、
それを上のように分解した !(T2) にも !(T4) は起きていないはずである。
よってあとは、(T1) である !(T2) が解消できればよい。
竹野茂治@新潟工科大学