![$\displaystyle
T[y^{2m}] = \frac{y}{2m+1}\left(y^{2m}-\frac{1}{2^{2m}}\right),
\hspace{1zw}
T[y^{2m-1}] = \frac{1}{2m}\left(y^{2m}-\frac{1}{2^{2m}}\right)$](img145.png) (23)
(23)
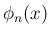 の計算を紹介する。
公式集や数式処理ソフトでも簡単に得られるかもしれないが、
ここでは少し地道な計算を示し、多項式としての形や
の計算を紹介する。
公式集や数式処理ソフトでも簡単に得られるかもしれないが、
ここでは少し地道な計算を示し、多項式としての形や 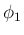 ,
, 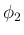 の
因数を出した形、および [T1],[T2] の形がどうなるかを紹介する。
の
因数を出した形、および [T1],[T2] の形がどうなるかを紹介する。
なお、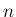 が奇数か偶数かで計算のしやすさに違いがあることに注意する。
例えば
が奇数か偶数かで計算のしやすさに違いがあることに注意する。
例えば 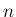 が奇数の場合は、[T2'] より
が奇数の場合は、[T2'] より
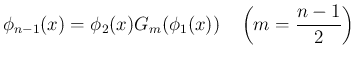
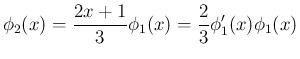
 を
とすれば、
を
とすれば、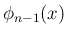 の積分は置換積分により、
の積分は置換積分により、
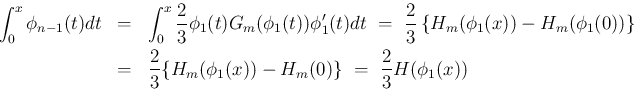
 が奇数の場合、
が奇数の場合、 の [T2'] の形が得られていれば、
そこから
の [T2'] の形が得られていれば、
そこから 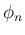 の [T1'] の形を得るのは難しくはなく、
ほぼ (24) の計算だけで済むし、
また、上の計算からもわかるが、
直接 (15) を使って計算しても、
の [T1'] の形を得るのは難しくはなく、
ほぼ (24) の計算だけで済むし、
また、上の計算からもわかるが、
直接 (15) を使って計算しても、
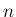 が奇数の場合は後ろの定積分の項は 0 となるため、
が奇数の場合は後ろの定積分の項は 0 となるため、
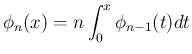
一方、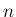 が偶数の場合は [T1'] の形から [T2'] を求めるのは
それほど易しくはない。(23) を使えば
一応計算できるのであるが、
が偶数の場合は [T1'] の形から [T2'] を求めるのは
それほど易しくはない。(23) を使えば
一応計算できるのであるが、
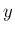 の多項式への変形や、
逆に
の多項式への変形や、
逆に 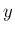 の式から
の式から 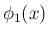 の式への展開などが入り、
の式への展開などが入り、
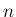 が奇数の場合よりも計算量が多くなる。
この場合はむしろ多項式として直接 (15) を使って計算し、
それを因数分解して [T2'] の形を作った方が、
が奇数の場合よりも計算量が多くなる。
この場合はむしろ多項式として直接 (15) を使って計算し、
それを因数分解して [T2'] の形を作った方が、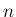 が大きい場合には
早いかもしれない。
が大きい場合には
早いかもしれない。
それでは、順に 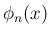 (
(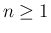 ) を計算する。
) を計算する。
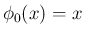 なので、定数
なので、定数 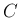 に対して
に対して
![$\displaystyle T[C] = \int_0^x Cdt + x\int_0^{-1}Cdt = Cx+x(-C) = 0
$](img160.png)
![\begin{eqnarray*}T[\phi_0]
&=& T[x]
\ =\ T\left[x+\frac{1}{2}\right]
\ =\ ...
...frac{1}{2}\right)^2-\frac{1}{4}\right\}
\ =\ \frac{1}{2}(x^2+x) \end{eqnarray*}](img161.png)
![$\displaystyle T[x]
= \int_0^x tdt + x\int_0^{-1} t dt
= \frac{x^2}{2}+\frac{x}{2}
$](img162.png)
![$\displaystyle \phi_1(x) = T[\phi_0] = \frac{x}{2}(x+1)
$](img163.png)
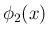 は、(23) を使えば、
は、(23) を使えば、
![\begin{eqnarray*}\phi_2(x)
&=&
2T[\phi_1(x)]
\ =\
T[x^2+x]
\ =\
T\left...
...ght)
\ = \
\frac{2x+1}{6}(x^2+x)
\ = \
\frac{x}{6}(x+1)(2x+1)\end{eqnarray*}](img165.png)
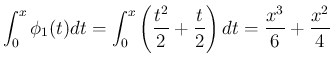
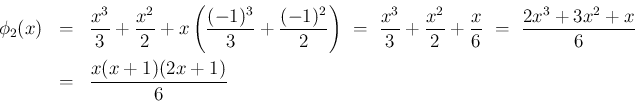
次は 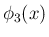 であるが、(25) を使うと、
この場合は
であるが、(25) を使うと、
この場合は 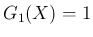 なので、
なので、
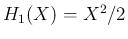 となり、よって
となり、よって
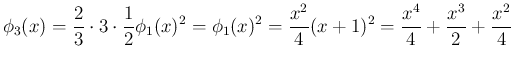
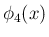 は、(23) で計算すると、
は、(23) で計算すると、
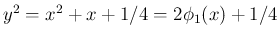 より、
より、
![\begin{eqnarray*}\phi_4(x)
&=&
4T[\phi_3(x)]
\ =\
T[(x^2+x)^2]
\ =\
T\l...
...+1)-\frac{\phi_2(x)}{2}
\ =\
\frac{\phi_2(x)}{5}(6\phi_1(x)-1)\end{eqnarray*}](img174.png)
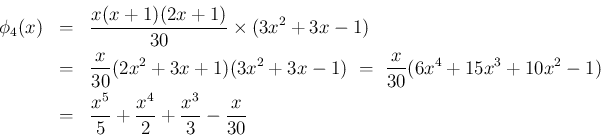
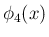 を直接 (15) から計算すれば、
を直接 (15) から計算すれば、
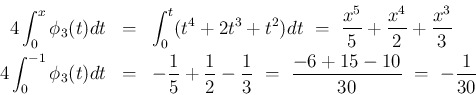
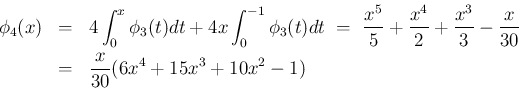
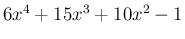 は
は 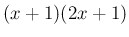 で割り切れるので、
実際に割り算を実行すれば、組み立て除法なら 3 行位の計算で済み、
で割り切れるので、
実際に割り算を実行すれば、組み立て除法なら 3 行位の計算で済み、
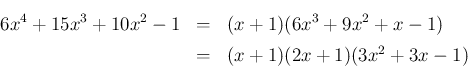
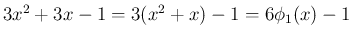 より、
前と同じものが得られることがわかる。
より、
前と同じものが得られることがわかる。
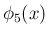 は、
は、
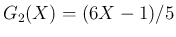 なので
なので
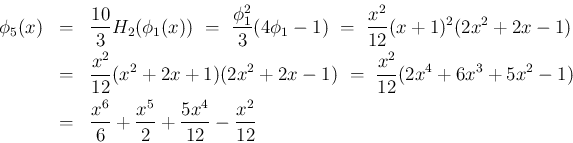
以下、計算結果のみを示す。紹介するのは、
ファウルハーバーの定理の形の式 ([T1'], [T2'])、
因数分解の形、および展開した式の 3 つの形である。
なお、因数分解式は、[T1'], [T2'] の形の 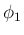 ,
, 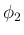 の
因数だけの因数分解式を紹介するが、
の
因数だけの因数分解式を紹介するが、
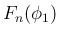 ,
, 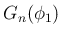 の部分が
さらに有理数係数の範囲で因数分解できるかもしれないが、
それは確認していない。
また、手計算での計算例なので、
計算間違いなどが含まれる可能性もある。
の部分が
さらに有理数係数の範囲で因数分解できるかもしれないが、
それは確認していない。
また、手計算での計算例なので、
計算間違いなどが含まれる可能性もある。
ここまでの式を見ると、これらの式にはさらに次の性質があることがわかる。
 を展開すると、次数の高い最初の 2 項は
以下のようになる:
を展開すると、次数の高い最初の 2 項は
以下のようになる:
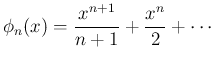
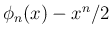 は、
は、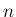 が偶数なら奇関数、
が偶数なら奇関数、
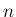 が奇数なら偶関数になる
が奇数なら偶関数になる
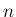 が 3 以上の奇数の場合、
が 3 以上の奇数の場合、
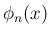 は
は 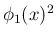 でも割り切れる
でも割り切れる
なお、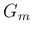 から
から 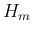 を計算する (24) と (25)、および [T1'] より、
を計算する (24) と (25)、および [T1'] より、
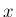 ,
, 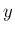 を介さずに
を介さずに 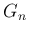 から 直接
から 直接 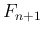 を求める式
を求める式
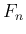 から
から 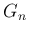 を直接求める式を作ることもできなくはないが、
その計算は、以下に示すようにあまり易しくはない。
を直接求める式を作ることもできなくはないが、
その計算は、以下に示すようにあまり易しくはない。
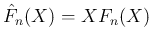 とすると、
とすると、
![$\displaystyle \phi_{2n}(x)
= 2nT\left[\phi_{2n-1}\right]
= 2nT\left[\hat{F}_n(\phi_1)\right]
$](img199.png)
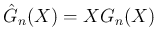 として、
として、
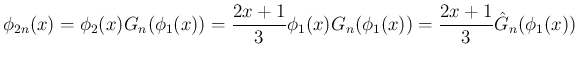
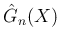 を求める微分方程式
が得られる。この左辺を
を求める微分方程式
が得られる。この左辺を 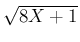 で割れば、
で割れば、
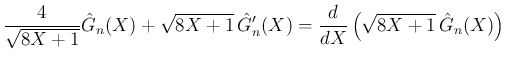
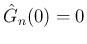 より、
より、
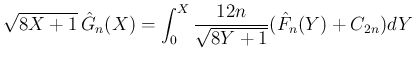
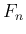 から
から 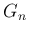 を計算する公式
が得られる。
左辺は
を計算する公式
が得られる。
左辺は 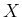 の多項式であるから、
定数
の多項式であるから、
定数 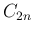 は、右辺の積分で平方根の式
は、右辺の積分で平方根の式 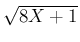 が
残らないように選べばよい。
が
残らないように選べばよい。
例えば、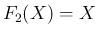 から (31) を用いて
から (31) を用いて
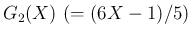 を計算してみる。
を計算してみる。
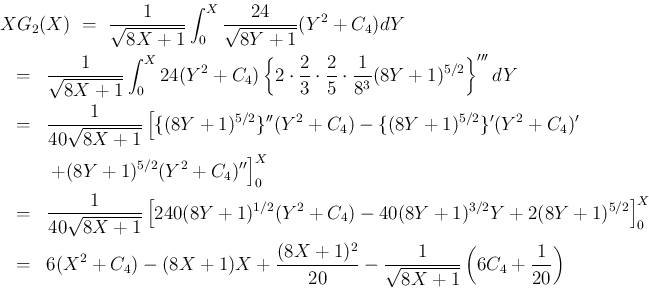
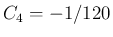 となり、
そのとき、
となり、
そのとき、
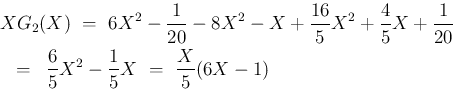
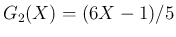 が得られるが、
計算は
が得られるが、
計算は  の計算 (26) に比べればかなり面倒で、
これで
の計算 (26) に比べればかなり面倒で、
これで  を計算をするのはあまり実用的ではない。
を計算をするのはあまり実用的ではない。
竹野茂治@新潟工科大学