5 関数表現
フィボナッチ数列の一般項を表す式 (2) は、
実はある関数を使ってある意味で一つの形にまとめることができる。
それを、まず別の例で簡単に紹介しよう。
特性方程式が複素数解を持つような次の 3 項漸化式を考える。
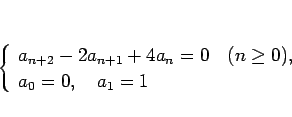 |
(25) |
この場合、特性方程式は

であるから解は、
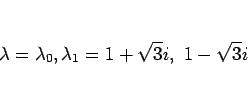
となる。よって、一般解は、
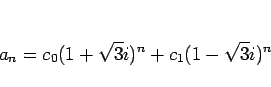
と書けるので、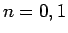 により
により
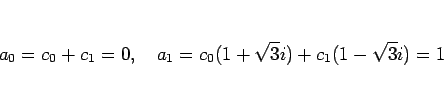
となるので、これを解けば

となるから、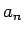 は、もちろん (25) より
すべての項が整数であるが、その一般項は
は、もちろん (25) より
すべての項が整数であるが、その一般項は  を用いて
を用いて
 |
(26) |
と表されることになる。
一方で、これを複素数を使わない表現にもできる。オイラーの公式を使えば、

となるので、一般解を

と三角関数により実数形で書くことができる。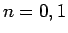 により
により
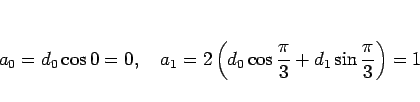
であるからこれを解いて
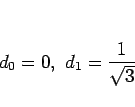
となるので、よって、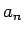 は
は
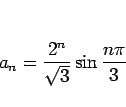 |
(27) |
と、 を使わずに書ける。
このように 2 つの等比数列の和による解 (26) が、
三角関数を使えば積による一つの式で表すことができる。
を使わずに書ける。
このように 2 つの等比数列の和による解 (26) が、
三角関数を使えば積による一つの式で表すことができる。
実はこれに似たことをフィボナッチ数列の解 (2) に対しても
行うことができる。
(2) は一見 (26) に似ていなくもないので、
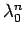 などを指数の形に書けば、
同様のことができるのではないかと想像されるだろう。今、
などを指数の形に書けば、
同様のことができるのではないかと想像されるだろう。今、
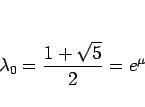
とすると、 は
は
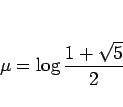
となり、このとき  は
は
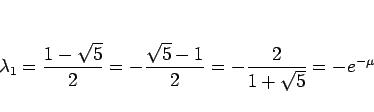
となるから、(2) は、
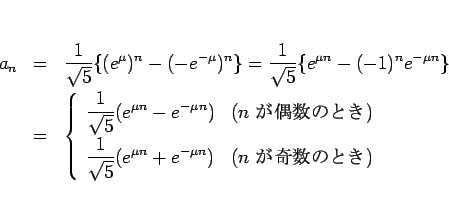
となるので、双曲線関数を使えば、
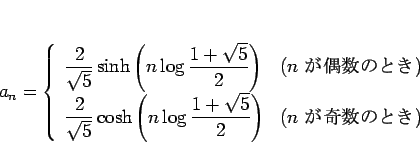 |
(28) |
と書けることになる。
もちろん、この式 (28) が (2) よりも
便利な式かというと必ずしもそうとは言えないだろうが、
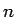 が一箇所に収まるという点で (28) の方が便利な場合ももしかしたらあるかもしれない。
が一箇所に収まるという点で (28) の方が便利な場合ももしかしたらあるかもしれない。
竹野茂治@新潟工科大学
2009年8月5日
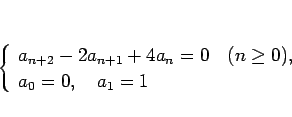
![]() などを指数の形に書けば、
同様のことができるのではないかと想像されるだろう。今、
などを指数の形に書けば、
同様のことができるのではないかと想像されるだろう。今、
![]() が一箇所に収まるという点で (28) の方が便利な場合ももしかしたらあるかもしれない。
が一箇所に収まるという点で (28) の方が便利な場合ももしかしたらあるかもしれない。