3 隣接積の和の最大最小
では、今度は 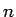 個のデータ
個のデータ
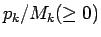 が
与えられたときに、(3) の
が
与えられたときに、(3) の 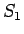 の値は、
軸の並べかえでどのように変化するか、
どのような並びのときに (3) の値は、
最大、最小となるのか、といったことを考えてみる。
の値は、
軸の並べかえでどのように変化するか、
どのような並びのときに (3) の値は、
最大、最小となるのか、といったことを考えてみる。
これは、
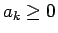 (
(
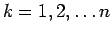 ) に対し、
) に対し、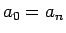 とするとき、
とするとき、
の値が、
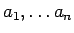 の順を並べかえたときに、
どのような並びのときに最大、あるいは最小となるか、という問題になる。
そのため、この
の順を並べかえたときに、
どのような並びのときに最大、あるいは最小となるか、という問題になる。
そのため、この 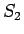 と、両端の積を排除した
と、両端の積を排除した
を考えてみることにする。
ここでは、数列のすべての並びかえを考えるので、元の 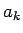 は
は
であるとしてよい。
簡単のため、例えば 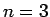 の場合を考えてみる。
まず
の場合を考えてみる。
まず 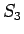 を考える。通常の
を考える。通常の 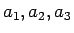 の並びに対しては、
の並びに対しては、
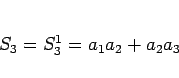 |
(4) |
となるが、これを並べかえて 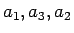 とすると、
とすると、 の値は
の値は
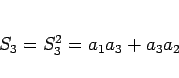 |
(5) |
となり、さらに 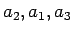 という並びに対しては、
という並びに対しては、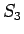 は
は
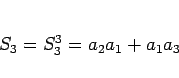 |
(6) |
となる。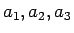 の順列の並べかえは
全部で
の順列の並べかえは
全部で 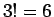 通りあるが、
並び全体を反転させても
通りあるが、
並び全体を反転させても 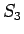 の値は変わらないので、
並べかえによる値はこの
の値は変わらないので、
並べかえによる値はこの 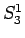 ,
, 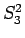 ,
, 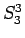 の 3 通りとなる。
例えば、
の 3 通りとなる。
例えば、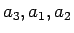 に対する
に対する 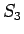 は確かに
は確かに
に等しくなる。
この 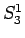 ,
, 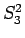 ,
, 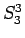 では、
では、
より
 で、また
で、また
より
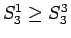 なので、
よって
なので、
よって
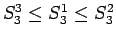 であり、
であり、
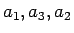 (および
(および 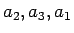 ) の並びの場合に
) の並びの場合に 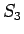 は最大、
は最大、
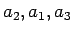 (および
(および 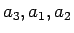 ) の並びの場合に最小となる
ことがわかる。
) の並びの場合に最小となる
ことがわかる。
一方 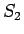 は、
は、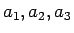 に対しては
に対しては
となるが、これも反転しても値は変わらないが巡回的、すなわち円順列なので、
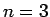 の場合は
の場合は 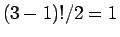 通り、
すなわちこの
通り、
すなわちこの 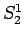 の 1 種類しかない。
の 1 種類しかない。
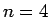 の場合は、
の場合は、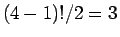 通りあり、
通りあり、
となる。他のものはすべてこのいずれかと同じものになる。
例えば、
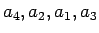 の場合は、
の場合は、
となる。
これらの大小は、
より
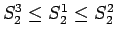 となり、
よって
となり、
よって
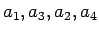 の並びのときに最小、
の並びのときに最小、
 の並びのときに最大となることがわかる。
の並びのときに最大となることがわかる。
なお、上の例では、すべての並べかえに対して 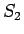 ,
, 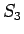 の大小が
の大小が
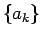 の順序から一意に確定している、
すなわち線形順序 (全順序) がついているが、
これは常にそうなるわけではない。
例えば、
の順序から一意に確定している、
すなわち線形順序 (全順序) がついているが、
これは常にそうなるわけではない。
例えば、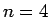 の
の 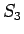 では、
では、
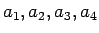 の並びに対する
の並びに対する
と、
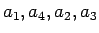 の並びに対する
の並びに対する
を比較すると、
となるが、これは正の項同士の差で、
その正負は
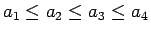 の大小だけでは決定せず、
値によって変わりうる。
例えば
の大小だけでは決定せず、
値によって変わりうる。
例えば 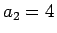 ,
, 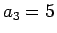 ,
, 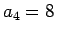 ,
, 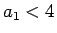 とすると、
とすると、
となるので、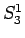 と
と 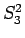 の大小は、
の大小は、
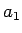 が 2 より大きいか小さいかで変わることになり、
が 2 より大きいか小さいかで変わることになり、
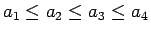 という条件だけでは必ずしも確定しない。
このように、すべての並びに必ずしも大小は確定はしないが、
しかし最大値、最小値を与える並びはこの後見るように常に確定する。
という条件だけでは必ずしも確定しない。
このように、すべての並びに必ずしも大小は確定はしないが、
しかし最大値、最小値を与える並びはこの後見るように常に確定する。
竹野茂治@新潟工科大学
2017年2月9日
![]() (
(
![]() ) に対し、
) に対し、![]() とするとき、
とするとき、
![]() は
は
![]() の場合を考えてみる。
まず
の場合を考えてみる。
まず ![]() を考える。通常の
を考える。通常の ![]() の並びに対しては、
の並びに対しては、
![]() は、
は、![]() に対しては
に対しては
![]() の場合は、
の場合は、![]() 通りあり、
通りあり、
![]() ,
, ![]() の大小が
の大小が
![]() の順序から一意に確定している、
すなわち線形順序 (全順序) がついているが、
これは常にそうなるわけではない。
例えば、
の順序から一意に確定している、
すなわち線形順序 (全順序) がついているが、
これは常にそうなるわけではない。
例えば、![]() の
の ![]() では、
では、
![]() の並びに対する
の並びに対する