5 3 次方程式の利用
本節で、3 乗根と平方根の 2 重根号 (1) を、
3 次方程式を利用して外す方法を紹介する。
基本的には、(7) のように
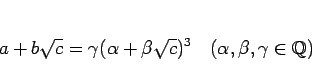 |
(22) |
となる 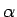 ,
, 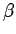 ,
, 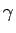 を見つけることが目標となるが、
(22) がもし成り立てば、
を見つけることが目標となるが、
(22) がもし成り立てば、
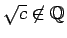 であることから、
であることから、
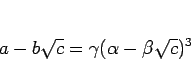 |
(23) |
となることもわかる (補題 9)。
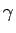 は、
は、
![$\sqrt[3]{a+b\sqrt{c}}$](img93.gif) と
と
![$\sqrt[3]{a-b\sqrt{c}}$](img94.gif) の積を
考えると、(22), (23) より
の積を
考えると、(22), (23) より
となるので、この積に現れる 3 乗根を消すようにその値を決めればよい。
このとき、(22), (23) より
となるが、この左辺が 3 次方程式の解の形をしているので、
これを解に持つ 3 次方程式を作り、
その解を 3 次式の因数分解で求め、そこから 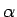 を定め、
それを手掛かりに
を定め、
それを手掛かりに 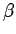 を求める、
という方向で 2 重根号を外すことができる。
を求める、
という方向で 2 重根号を外すことができる。
その手順を具体的な例で 2, 3 示す。
まずは、
を考える。これに対して、
とすると、
となって 3 乗根が残らないので、この場合は 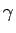 は
必要ない (
は
必要ない (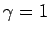 )。
また、
)。
また、
なので、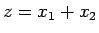 とすると、
とすると、
となり、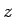 は 3 次方程式
は 3 次方程式
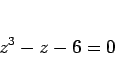 |
(24) |
を満たすことがわかる。
この式の左辺に 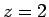 を代入すると 0 になるので、
(24) の左辺は
を代入すると 0 になるので、
(24) の左辺は
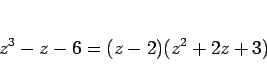 |
(25) |
と因数分解され、よって (24) の解は
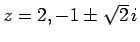 となり、
実数である
となり、
実数である 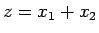 は 2 に等しいことがわかる。
は 2 に等しいことがわかる。
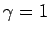 だったので、
だったので、
より 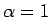 となる。よって、
となる。よって、
と展開すると、
となり、前者より
と求まるが、これは後者も確かに満たしている。
これで、
と 2 重根号が外せることになる。ついでに、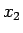 も
も
となることがわかる。
例えば、
![$\sqrt[3]{2+\sqrt{5}}$](img116.gif) なども同様にして 2 重根号を外すことができる。
なども同様にして 2 重根号を外すことができる。
次は、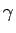 が必要な場合として、今の
が必要な場合として、今の 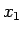 の分母を払った、
の分母を払った、
![\begin{displaymath}
x_3 = \sqrt[3]{27+11\sqrt{6}}\end{displaymath}](img118.gif) |
(26) |
を考える。この場合、
とすると、
と 3 乗根が残るが、これを消すように 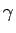 を設定する。
この場合は
を設定する。
この場合は
あるいは、
を 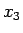 ,
, 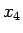 の代わりに考えればよい。こうすれば、
の代わりに考えればよい。こうすれば、
となって 3 乗根が消えるからである。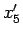 ,
, 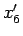 の方は
この先の計算は
の方は
この先の計算は 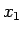 ,
, 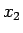 と同じなので、
ここでは
と同じなので、
ここでは 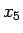 ,
, 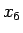 で計算してみる。
で計算してみる。
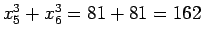 なので、
なので、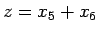 とすると
とすると
より、
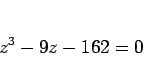 |
(27) |
を得る。なお、これは
の形をしているので、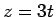 として両辺を
として両辺を 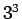 で割ると
で割ると
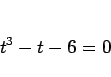 |
(28) |
と直すことができる。
(27) が有理数の範囲で因数分解できることと、
(28) が有理数の範囲で因数分解できることは
同等であり、よって因数分解は後者を考えればよい。
(25) により、結局 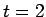 で、
で、
であることがわかる。よってこの場合は 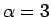 であり、
であり、
より、
から 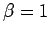 が得られる。
これで、
が得られる。
これで、
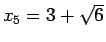 となり、結局
となり、結局
![\begin{displaymath}
x_3 = \frac{x_5}{\sqrt[3]{3}}
= \frac{3+\sqrt{6}}{\sqrt[3]{3}}
\left(=\sqrt[3]{9} + \sqrt[6]{24}\right)\end{displaymath}](img145.gif) |
(29) |
の形に (26) の 2 重根号が外せたことになる。
例えば、
![$\sqrt[3]{5+3\sqrt{3}}$](img146.gif) なども同様にして 2 重根号を外すことができる。
なども同様にして 2 重根号を外すことができる。
最後に、2 重根号が外せない例も紹介しておく。
とする。これに対して
とすると、
となるので、
(あるいは
![$x_9'=x_7/\sqrt[3]{2}$](img151.gif) ,
,
![$x_{10}'=x_8/\sqrt[3]{2}$](img152.gif) でもよい) とすると
でもよい) とすると
なので、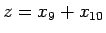 とすると
とすると
より
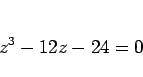 |
(30) |
となり、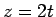 とすして 8 で割れば
とすして 8 で割れば
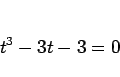 |
(31) |
が得られる (
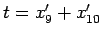 に対応する)。
に対応する)。
この (31) の左辺を有理数の範囲で
因数分解するのであるが、
それは整数係数の多項式で因数分解される必要があり (6.1 節、補題 5 参照)、
よって 1 次因数として 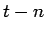 (
(
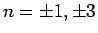 ) の形の式を
持たなければならない (6.3 節参照)。
ところが、
) の形の式を
持たなければならない (6.3 節参照)。
ところが、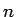 として
として 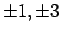 の
いずれを (31) の左辺に代入しても 0 にはならないので、このような因数はないことがわかる。
よって (31)、
そして (30) は
有理数の範囲では因数分解ができないことになる。
の
いずれを (31) の左辺に代入しても 0 にはならないので、このような因数はないことがわかる。
よって (31)、
そして (30) は
有理数の範囲では因数分解ができないことになる。
これにより、
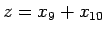 は 3 乗根が外れることはなく (外れれば
は 3 乗根が外れることはなく (外れれば 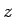 は有理数になるはず)、
よって、
は有理数になるはず)、
よって、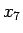 ,
, 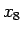 の 2 重根号も外すことができないことがわかる。
の 2 重根号も外すことができないことがわかる。
ここまでの方法をまとめると、以下のようになる。
-
![$X=\sqrt[3]{a+b\sqrt{c}}$](img167.gif) に対して
に対して
![$Y=\sqrt[3]{a-b\sqrt{c}}$](img168.gif) とし、
とし、
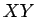 を計算する
を計算する
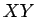 に 3 乗根
に 3 乗根 ![$\sqrt[3]{p}$](img170.gif) が残る場合は、
が残る場合は、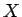 ,
, 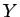 の代わりに
の代わりに
![$X'=\sqrt[3]{p}X$](img173.gif) ,
,
![$Y'=\sqrt[3]{p}Y$](img174.gif) を考える (それを改めて
を考える (それを改めて 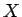 ,
, 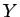 とする)
とする)
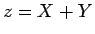 として、
として、
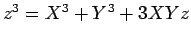 により
により 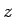 が満たす
有理数係数の 3 次方程式を求める
が満たす
有理数係数の 3 次方程式を求める
- それが有理数の範囲で因数分解できなければ
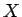 の 2 重根号は
外すことができず、因数分解できればその実数解が
の 2 重根号は
外すことができず、因数分解できればその実数解が 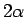 となる
となる
-
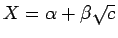 として、
これを 3 乗して係数比較することで
として、
これを 3 乗して係数比較することで 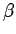 を求め、
これで
を求め、
これで 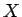 の 2 重根号が外される
の 2 重根号が外される
- 2. を行った場合は、5. の結果を
![$\sqrt[3]{p}$](img170.gif) で割ることで
で割ることで 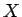 が求まる
が求まる
竹野茂治@新潟工科大学
2018-03-02
![]() なども同様にして 2 重根号を外すことができる。
なども同様にして 2 重根号を外すことができる。
![]() が必要な場合として、今の
が必要な場合として、今の ![]() の分母を払った、
の分母を払った、
![]() なので、
なので、![]() とすると
とすると
![]() なども同様にして 2 重根号を外すことができる。
なども同様にして 2 重根号を外すことができる。
![]() (
(
![]() ) の形の式を
持たなければならない (6.3 節参照)。
ところが、
) の形の式を
持たなければならない (6.3 節参照)。
ところが、![]() として
として ![]() の
いずれを (31) の左辺に代入しても 0 にはならないので、このような因数はないことがわかる。
よって (31)、
そして (30) は
有理数の範囲では因数分解ができないことになる。
の
いずれを (31) の左辺に代入しても 0 にはならないので、このような因数はないことがわかる。
よって (31)、
そして (30) は
有理数の範囲では因数分解ができないことになる。
![]() は 3 乗根が外れることはなく (外れれば
は 3 乗根が外れることはなく (外れれば ![]() は有理数になるはず)、
よって、
は有理数になるはず)、
よって、![]() ,
, ![]() の 2 重根号も外すことができないことがわかる。
の 2 重根号も外すことができないことがわかる。