2 設定
問題の設定として、[1] と同じ、以下のものを仮定する。
- 仮定 1:
目標は、代金の支払いで、おつりの枚数を減らすことではなく、
最終的に財布に残る小銭の枚数をなるべく少なくすること。
- 仮定 2:
お札の枚数は考慮しないし、代金を払うには十分なお札も持っている。
- 仮定 3:
代金を支払う前の財布の中には無駄な小銭はない。
すなわち、(日本の硬貨系では) 1 円、10 円、100 円硬貨は
それぞれ最大で 4 枚まで、
5 円、50 円、500 円硬貨はそれぞれ最大で 1 枚しかない。
- 仮定 4:
おつりを返す店側には、
すべての種類の硬貨が十分な枚数揃っていて、
店員は枚数が最も少なくなるようにおつりを返す。
- 仮定 5:
支払う硬貨の一部が、そのままおつりの一部として戻ってくる
払い方はしない。
なお、考える硬貨系は、[1] と同じ、一般化した硬貨系とする。
すなわち、
の額の硬貨が、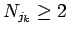 (
(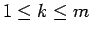 ) に対して
) に対して
を満たし、札の金額 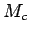 は
は
であるとする。この場合各硬貨 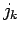 の必要枚数は
の必要枚数は 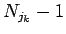 枚で、
それに対して、[1] の命題 1, 2 が成り立つ。
枚で、
それに対して、[1] の命題 1, 2 が成り立つ。
- 命題 1. ([1])
-
この硬貨系では、各硬貨の必要枚数以内で 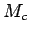 未満の金額は
すべて表現でき、そしてそのような表現は一意的である。
未満の金額は
すべて表現でき、そしてそのような表現は一意的である。
- 命題 2. ([1])
-
必要枚数以内という制限を外して考えた場合、
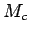 未満の金額の表現は、常に必要枚数以内の表現が枚数は最小となり、
その最小を与える表現は一意的に決定する。
未満の金額の表現は、常に必要枚数以内の表現が枚数は最小となり、
その最小を与える表現は一意的に決定する。
この命題 1, 2 は、この硬貨系の基本的な命題であり、
本稿では中心的な役割を果たす。
命題 1 の証明はそれほど長くはないし難しくもない ([1] 参照)。
命題 2 も、必要枚数を越えている表現は両替して
より少ない枚数の表現に変換できることを考えれば、
命題 1 から導くのは難しくはない。
なお、今後この硬貨系の必要枚数以下の小銭しかない状態を、
「冗長性がない」と呼ぶことにする。
竹野茂治@新潟工科大学
2017年12月20日
![]() 未満の金額は
すべて表現でき、そしてそのような表現は一意的である。
未満の金額は
すべて表現でき、そしてそのような表現は一意的である。
![]() 未満の金額の表現は、常に必要枚数以内の表現が枚数は最小となり、
その最小を与える表現は一意的に決定する。
未満の金額の表現は、常に必要枚数以内の表現が枚数は最小となり、
その最小を与える表現は一意的に決定する。