5 基本的な事実
この節では、硬貨系の支払いとおつり等に関する
基本的な事実をいくつか取り上げていく。
- 命題 2.
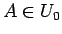 ,
, 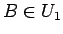 が
が
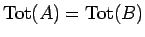 であれば、
であれば、
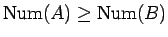 となる。
さらに、この等号が成り立つのは
となる。
さらに、この等号が成り立つのは 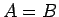 のときのみである。
のときのみである。
これは、同じ額では、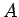 のように仮定 3 を満たさない
硬貨の集まりよりも、仮定 3 を満たす集まりの方が
硬貨の枚数は少なくなることを意味する。
のように仮定 3 を満たさない
硬貨の集まりよりも、仮定 3 を満たす集まりの方が
硬貨の枚数は少なくなることを意味する。
例えば、同じ 552 円を表す組は、
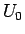 でなら 10 円玉 5 枚以上も使えるし、
100 円玉も 5 枚以上使えるので色々あるが、
その枚数が最小になるのは、
でなら 10 円玉 5 枚以上も使えるし、
100 円玉も 5 枚以上使えるので色々あるが、
その枚数が最小になるのは、
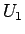 の 500 円玉 1 枚、50 円玉 1 枚、1 円玉 2 枚、
になることを意味する。
の 500 円玉 1 枚、50 円玉 1 枚、1 円玉 2 枚、
になることを意味する。
命題 2 の一般の場合を証明する前に、
簡単な例として 1 円玉、5 円玉、10 円玉の 3 種類だけの場合を考える。
この場合命題 2 は、
| |
|
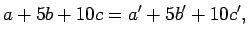 |
(13) |
| |
|
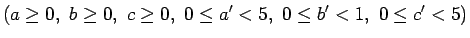 |
|
のときに、
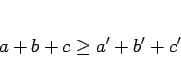 |
(14) |
であることを意味する。
(13) を 5 で割った余りを考えれば、
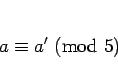
となり、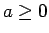 ,
, 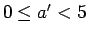 より
より
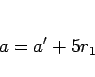 |
(15) |
となる 0 以上の整数 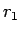 が存在することになる。
これは、すなわち
が存在することになる。
これは、すなわち 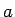 のうち
のうち 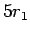 円分の 1 円玉は
円分の 1 円玉は 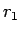 個の
5 円玉で置きかえられることを意味する。
個の
5 円玉で置きかえられることを意味する。
(15) を (13) に代入して整理すれば、
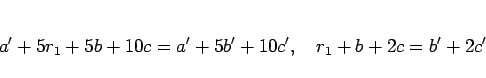
となるので、最後の式を 2 で割った余りで考えれば、上と同様にして
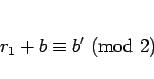
より
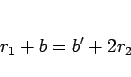 |
(16) |
となる 0 以上の整数 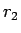 が存在する。
これは、
が存在する。
これは、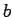 個の 5 円玉と、
個の 5 円玉と、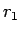 個の 5 円玉分の 1 円玉の集まりのうち、
個の 5 円玉分の 1 円玉の集まりのうち、
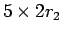 円分は
円分は 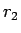 個の 10 円玉で置きかえられることを意味する。
個の 10 円玉で置きかえられることを意味する。
(16) を上の式に代入すれば、
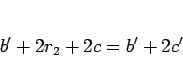
より
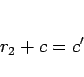 |
(17) |
となる。
これは、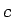 個の 10 円玉と
個の 10 円玉と 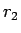 個の 10 円玉分の下からの繰り上がりが
個の 10 円玉分の下からの繰り上がりが
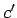 個の 10 円玉に等しいことを意味する。
個の 10 円玉に等しいことを意味する。
(15), (16), (17) を辺々加えると、
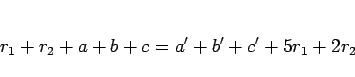
となるので、
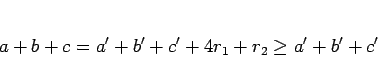
であることがわかる。しかも、等号が成り立つのは 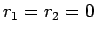 の
ときであるから、
(15), (16), (17) より
の
ときであるから、
(15), (16), (17) より
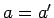 ,
, 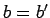 ,
, 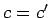 のときであることがわかる。
のときであることがわかる。
一般の場合も、これと同様の考察を行えば、
命題 2 が証明できる。
証明 (命題 2)
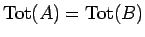 より
より
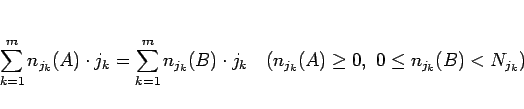 |
(18) |
(10) より、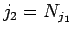 で割った余りを考えると、
で割った余りを考えると、
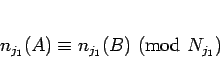
より、
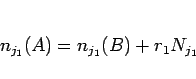 |
(19) |
となる 0 以上の整数 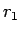 が存在する。
これを (18) に代入し、
両辺から
が存在する。
これを (18) に代入し、
両辺から 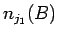 を引き、
を引き、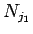 で割ると、
(12) より
で割ると、
(12) より
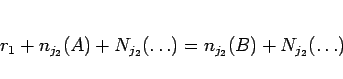
のような形になるので、これを 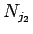 で割った余りを考えると、
で割った余りを考えると、
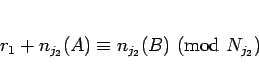
なので、
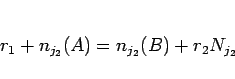
となる 0 以上の整数 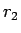 が存在する。
この作業を繰り返すと、結局
が存在する。
この作業を繰り返すと、結局  の
の 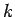 に対し
に対し
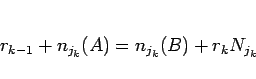 |
(20) |
となるような 0 以上の整数 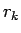 が存在し、さらに
が存在し、さらに
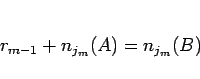 |
(21) |
となる。
(19),
(20),
(21) を辺々加えると、
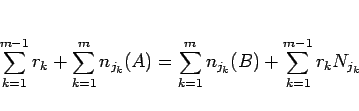
となるので、よって
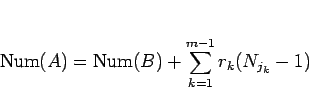 |
(22) |
となるので、
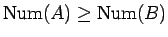 が成り立つ。
が成り立つ。
さらに、
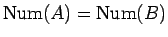 となるのは、
となるのは、
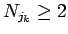 よりすべての
よりすべての 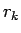 が 0 になることと同値で、
それは、
(19),
(20),
(21) より
すべての
が 0 になることと同値で、
それは、
(19),
(20),
(21) より
すべての 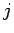 に対して
に対して 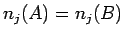 であることと同じ、
すなわち
であることと同じ、
すなわち 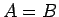 と同じであることがわかる。
と同じであることがわかる。
以後、主に 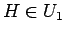 を財布の小銭全部、
を財布の小銭全部、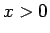 を代金、
を代金、
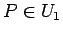 を支払う小銭 (必要な場合はこれに
を支払う小銭 (必要な場合はこれに 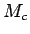 円の額のお札を
追加する場合もある)、
円の額のお札を
追加する場合もある)、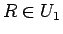 をおつりの小銭、とする。
をおつりの小銭、とする。
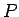 と
と 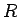 は仮定 5 を満たさなければいけないので、
各硬貨成分
は仮定 5 を満たさなければいけないので、
各硬貨成分 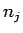 に対して、
に対して、
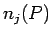 と
と 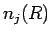 のいずれかが必ず 0 でなければならない。
すなわち、すべての
のいずれかが必ず 0 でなければならない。
すなわち、すべての 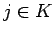 に対して
に対して
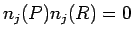 となるので、
通常のベクトルと同じように内積を
となるので、
通常のベクトルと同じように内積を
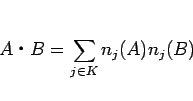 |
(23) |
と定めると、この仮定 5 の条件は、
簡単に
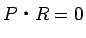 と書くことができる。
と書くことができる。
逆に、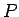 ,
, 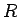 が
が
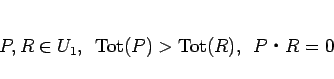 |
(24) |
を満たしているとき、
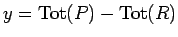 とすると、
とすると、
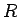 は代金
は代金 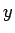 に対して
に対して 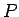 を支払ったおつりと見ることができる。
実際、
を支払ったおつりと見ることができる。
実際、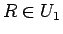 より
より 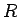 は仮定 4 を満たすし、
は仮定 4 を満たすし、
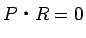 より仮定 5 も満たされていて、
金額的にも適合する。
すなわち、支払いとおつりは (24) の関係を満たすことが
互いの条件であることがわかる。
より仮定 5 も満たされていて、
金額的にも適合する。
すなわち、支払いとおつりは (24) の関係を満たすことが
互いの条件であることがわかる。
- 命題 3.
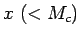 が代金、
が代金、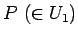 が支払い、
が支払い、
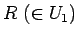 がおつりの場合、
がおつりの場合、
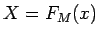 とすると、
とすると、
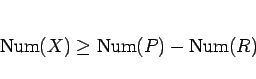 |
(25) |
が成り立つ。等号成立は
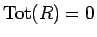 のときで、かつこのときに限る。
のときで、かつこのときに限る。
これは例えば、代金が 72 円で、支払いが 122 円、
おつりが 50 円の場合を考えると、
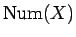 は 50 円玉 1 枚、10 円玉 2 枚、1 円玉 2 枚より 5 枚、
は 50 円玉 1 枚、10 円玉 2 枚、1 円玉 2 枚より 5 枚、
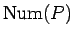 は 100 円玉 1 枚、10 円玉 2 枚、1 円玉 2 枚より 5 枚、
は 100 円玉 1 枚、10 円玉 2 枚、1 円玉 2 枚より 5 枚、
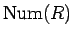 は 50 円玉 1 枚なので、
は 50 円玉 1 枚なので、
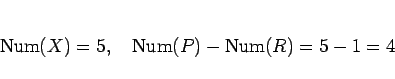
となり、(25) が成り立つ。
この命題 3 からすぐに次の系が得られる。
- 系 4.
- 丁度の代金を払える場合はそれが最適解であり、それは一意的である。
すなわち、おつりをもらう場合は、
丁度の代金の場合の小銭の枚数よりも
必ず減らせる小銭の枚数は少なくなる。
命題 3 は、命題 2 から容易に
示されるが、その証明のため、次の記号を導入する:
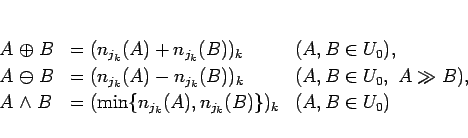
証明 (命題 3)
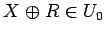 の定義から明らかに、
の定義から明らかに、
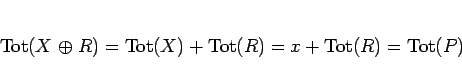
であるから、命題 2 より、
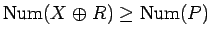 となるが、
定義より明らかに
となるが、
定義より明らかに
 なので、
なので、
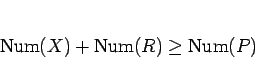
となり、(25) が成り立つ。
また、等号が成り立つのは、
命題 2 より
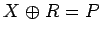 となる場合であるが、
(24) より
となる場合であるが、
(24) より
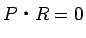 でなければいけないので、
でなければいけないので、
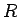 の成分はすべて 0 でなければならない。よって、
の成分はすべて 0 でなければならない。よって、
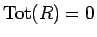 となる。
となる。
逆に
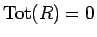 、すなわちおつりがなければ、もちろん等号となる。
、すなわちおつりがなければ、もちろん等号となる。
竹野茂治@新潟工科大学
2014年11月19日
![]() でなら 10 円玉 5 枚以上も使えるし、
100 円玉も 5 枚以上使えるので色々あるが、
その枚数が最小になるのは、
でなら 10 円玉 5 枚以上も使えるし、
100 円玉も 5 枚以上使えるので色々あるが、
その枚数が最小になるのは、
![]() の 500 円玉 1 枚、50 円玉 1 枚、1 円玉 2 枚、
になることを意味する。
の 500 円玉 1 枚、50 円玉 1 枚、1 円玉 2 枚、
になることを意味する。
![]() より
より
![]() となるのは、
となるのは、
![]() よりすべての
よりすべての ![]() が 0 になることと同値で、
それは、
(19),
(20),
(21) より
すべての
が 0 になることと同値で、
それは、
(19),
(20),
(21) より
すべての ![]() に対して
に対して ![]() であることと同じ、
すなわち
であることと同じ、
すなわち ![]() と同じであることがわかる。
と同じであることがわかる。
![]() を財布の小銭全部、
を財布の小銭全部、![]() を代金、
を代金、
![]() を支払う小銭 (必要な場合はこれに
を支払う小銭 (必要な場合はこれに ![]() 円の額のお札を
追加する場合もある)、
円の額のお札を
追加する場合もある)、![]() をおつりの小銭、とする。
をおつりの小銭、とする。
![]() と
と ![]() は仮定 5 を満たさなければいけないので、
各硬貨成分
は仮定 5 を満たさなければいけないので、
各硬貨成分 ![]() に対して、
に対して、
![]() と
と ![]() のいずれかが必ず 0 でなければならない。
すなわち、すべての
のいずれかが必ず 0 でなければならない。
すなわち、すべての ![]() に対して
に対して
![]() となるので、
通常のベクトルと同じように内積を
となるので、
通常のベクトルと同じように内積を
![]() ,
, ![]() が
が
![]() の定義から明らかに、
の定義から明らかに、
![]() となる場合であるが、
(24) より
となる場合であるが、
(24) より
![]() でなければいけないので、
でなければいけないので、
![]() の成分はすべて 0 でなければならない。よって、
の成分はすべて 0 でなければならない。よって、
![]() となる。
となる。
![]() 、すなわちおつりがなければ、もちろん等号となる。
、すなわちおつりがなければ、もちろん等号となる。