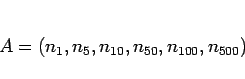 |
(1) |
(1)
なお、後でより一般の硬貨系の考察も可能なように、 以下のように (1) を一般化しておく:
(2)
(3)
(4)
(5)
このようなベクトル全体の集合を ![]() とし、
そのうち仮定 3 を満たすベクトル全体を
とし、
そのうち仮定 3 を満たすベクトル全体を ![]() と
書くこととする:
と
書くこととする:
(6)
ひとつの小銭の集まり (ベクトル) ![]() に対して、
各硬貨の枚数 (各成分)
に対して、
各硬貨の枚数 (各成分) ![]() が
が ![]() の成分であることを
明示するときは
の成分であることを
明示するときは
小銭の集まり ![]() に対して、
その小銭の表す合計金額を
に対して、
その小銭の表す合計金額を
![]() 、
その小銭の合計枚数を
、
その小銭の合計枚数を
![]() とする:
とする:
(7)
1000 円 (=![]() とする) 未満の金額
とする) 未満の金額 ![]() に対して、
その金額を
に対して、
その金額を ![]() のベクトルとして一意に表現する
小銭の集まりを
のベクトルとして一意に表現する
小銭の集まりを ![]() と書くことにする:
と書くことにする:
![]() に大小関係
に大小関係 ![]() (
(![]() ) を、次のように導入する:
) を、次のように導入する:
これら以外にも必要な記号があれば、適宜導入していく。
竹野茂治@新潟工科大学