log や sin などは、![]() のようなカッコのついた書き方、
すなわち
のようなカッコのついた書き方、
すなわち ![]() や
や ![]() のような書き方はせず、
慣習によりカッコは使わずに
のような書き方はせず、
慣習によりカッコは使わずに ![]() ,
, ![]() のように
書くことになっている。
さらに、それぞれに単項式を代入した場合も通常はカッコは書かずに
のように
書くことになっている。
さらに、それぞれに単項式を代入した場合も通常はカッコは書かずに
そこで問題になるのが、
例えば「![]() 」と「
」と「![]() 」の積のような場合である。
これに対して、次のような 9 つの書き方をあげてみる:
」の積のような場合である。
これに対して、次のような 9 つの書き方をあげてみる:
1. 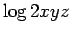 2.
2. 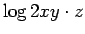 3.
3. 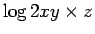
4. 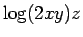 5.
5. 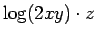 6.
6. 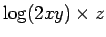
7. 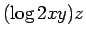 8.
8. 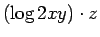 9.
9. 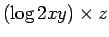
もちろん、これ以外に、
まず 1. は、もちろん ![]() との区別がつかないので論外であるが、
2., 3. と 1. との違いはかなり微妙な気がする。
との区別がつかないので論外であるが、
2., 3. と 1. との違いはかなり微妙な気がする。
中学で、数式の中の積の記号 ![]() は省略できる、と習うため、
積を意味する
は省略できる、と習うため、
積を意味する ![]() 、およびその代用である
、およびその代用である ![]() は、
は、
![]() ,
, ![]() のように、
主に数字同士の積の際に用いられる程度になる。
のように、
主に数字同士の積の際に用いられる程度になる。
余談であるが、同じ理由のために中学以降では
![]() (2 と 3/4 の和) のような帯分数は
積とまぎらわしいので使われなくなるが、特定の分野で使っているのか、
この書き方を使う学生が、例年少数ではあるがポツポツ見られる。
(2 と 3/4 の和) のような帯分数は
積とまぎらわしいので使われなくなるが、特定の分野で使っているのか、
この書き方を使う学生が、例年少数ではあるがポツポツ見られる。
このため、1. と 2., 3. との違いを説明するのは あまりやさしくはないと思う (少なくとも私にはできそうにはない) のだが、 この 2., 3. のような書き方が大学生用の多くの教科書で実際に使われている。 つまり、これがある種の慣用的な書き方であるらしい。
これに対し、4., 5., 6. は log にカッコを書くようにすることで、
関数に代入されているのは ![]() のみ、と一見明示しているようだが、
まだあいまいさが残る。
のみ、と一見明示しているようだが、
まだあいまいさが残る。
もし、コンピュータプログラムのように、
すべての対数を ![]() のようにカッコをつけて書くことにするならば、
4., 5., 6. で
のようにカッコをつけて書くことにするならば、
4., 5., 6. で ![]() は関数の外だとわかることになるが、
実際はそういう書き方が普通には行われていない以上、
そうは思ってもらえない可能性は十分ある。
また、ある授業だけ
は関数の外だとわかることになるが、
実際はそういう書き方が普通には行われていない以上、
そうは思ってもらえない可能性は十分ある。
また、ある授業だけ ![]() のように書くこととすることは、
特に
のように書くこととすることは、
特に ![]() を初めて学ぶ人に対しては教育的とは言えず、
もしそういう書き方に慣れてしまったら
他の人と正しい式のやり取りができなくなってしまう可能性を
生んでしまうことになるので、
そのように教えることには少し抵抗を感じる。
を初めて学ぶ人に対しては教育的とは言えず、
もしそういう書き方に慣れてしまったら
他の人と正しい式のやり取りができなくなってしまう可能性を
生んでしまうことになるので、
そのように教えることには少し抵抗を感じる。
7., 8., 9. であれば、誰もが間違えることなく ![]() は対数の外にあることがわかると思うし、
log の後ろの単項式にはカッコをつけない、
という慣用表現にも合致するので、
本来は 7., 8., 9. が一番自然だろうと思うし、
逆にこれらのカッコを 1., 2., 3. のように
容易に省略してよいものだとは思わない。
は対数の外にあることがわかると思うし、
log の後ろの単項式にはカッコをつけない、
という慣用表現にも合致するので、
本来は 7., 8., 9. が一番自然だろうと思うし、
逆にこれらのカッコを 1., 2., 3. のように
容易に省略してよいものだとは思わない。
同じ理由で、
そして、最初の方にも書いたが、 こういった問題を避けるために、 高校の教科書でも大学の教科書でも、実はむしろ
しかし、学生、特に初学者にはそのような背景はわからないので、
なぜ式の前後を入れ替えて ![]() や
や ![]() を前に出しているのかは、
式変形を見ただけでは理解しにくいのではないだろうか。
そして、そのような人が前出しの式を見ると、
「積の順序を入れ替えて前出しすることでカッコは省略できる」
と思うのではなく、単に、
「カッコは書かなくていいのね」と誤解してしまうことの方が多いような気がする。
を前に出しているのかは、
式変形を見ただけでは理解しにくいのではないだろうか。
そして、そのような人が前出しの式を見ると、
「積の順序を入れ替えて前出しすることでカッコは省略できる」
と思うのではなく、単に、
「カッコは書かなくていいのね」と誤解してしまうことの方が多いような気がする。
例えば以下のような正答例があるとしよう:
「の導関数を合成関数の微分法で求めると、
と置けば
なので、
なお三角関数には、もう一つ解消しがたい問題がある。
三角関数の慣用記法として、![]() と
と ![]() の積にもカッコを使わず、
の積にもカッコを使わず、
「log, sin には単項式が入る場合にはカッコはいらず、 逆にそれ以外の場合はカッコが必要になる」と考えるなら、
逆に、「![]() 」の書き方を認めると
「単項式にはカッコがいらない」ということが通らなくなってしまうが、
無理矢理屁理屈をつけるとすれば、
」の書き方を認めると
「単項式にはカッコがいらない」ということが通らなくなってしまうが、
無理矢理屁理屈をつけるとすれば、
「log 型関数同士は同レベルと見て、 そしてそこで一旦単項式からは切れることにする」などとなるかもしれない。しかし、これもやや苦しく、例えば
ちなみに、コンピュータプログラムでは、
log(x), sin(2*x*y)のように、関数名の後ろに必ずカッコを書く記法を取るので、 普通の数式に現れるようなあいまいさはなく、
log(x)*y (のようになる。 私自身もコンピュータプログラムを書くせいか、 個人的には慣用記法よりもこのような記法の方があいまいさを排除でき、 誤解も起こらず、正誤の判断もしやすいので、 ずっと良いのではないかと感じる。), log(2*x*y)*z (
),
sin(2*x)*sin(2*y) ()
竹野茂治@新潟工科大学