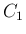
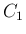 に対する前節の設定のもとで、
に対する前節の設定のもとで、
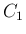 から
から 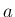 だけ外側に離れた曲線
だけ外側に離れた曲線 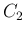 のパラメータ表示を考える。
のパラメータ表示を考える。
まず、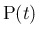 での外向き単位法線ベクトル
での外向き単位法線ベクトル
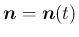 を
求める。
を
求める。
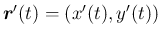 は
は 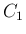 の接ベクトルで、
の接ベクトルで、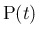 の
進行方向を向く。
よって
の
進行方向を向く。
よって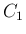 の外側は
の外側は
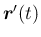 の右側になり、
の右側になり、
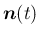 は
は
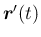 を時計回りに
を時計回りに 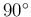 回転したベクトル
回転したベクトル
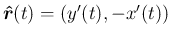 と同じ方向を向くので、
と同じ方向を向くので、
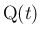 の軌跡を
の軌跡を 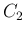 とすると (図 8)、
これが
とすると (図 8)、
これが 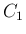 から
から 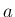 だけ離れた曲線の候補となる。
あとは実際に
だけ離れた曲線の候補となる。
あとは実際に 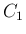 と
と 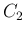 の距離がすべての点で
の距離がすべての点で 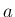 となることを
示せばよい。
となることを
示せばよい。
まず、
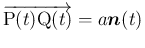 が、
が、
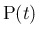 で
で 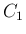 に垂直なだけでなく、
に垂直なだけでなく、
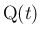 で
で 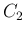 にも垂直であることを示す。
そのためには、
にも垂直であることを示す。
そのためには、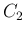 の
の 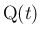 での接ベクトル
での接ベクトル
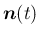 と垂直であることを示せばよい。
と垂直であることを示せばよい。
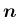 と
と
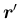 は垂直なので、
(9) よりあとは
は垂直なので、
(9) よりあとは
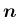 と
と
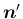 が垂直で
あることを示せばよいが、
が垂直で
あることを示せばよいが、
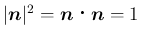 なので、
これを
なので、
これを 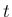 で微分すれば、
で微分すれば、
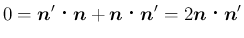
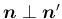 がわかる。これで、
がわかる。これで、
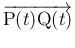 が、
が、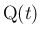 で
で 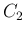 にも
垂直であることがわかった。
にも
垂直であることがわかった。
これを用いて、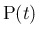 と
と 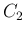 上の点で最短距離に
あるのが
上の点で最短距離に
あるのが 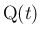 であることを示す。
逆に、
であることを示す。
逆に、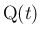 以外に
以外に 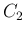 上に
上に 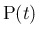 との距離が
より近い点
との距離が
より近い点 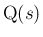 があったとする (
があったとする (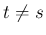 )。
もし、
)。
もし、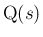 で
で
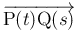 が
が 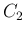 と
垂直でなければ、
と
垂直でなければ、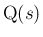 の付近で、より
の付近で、より 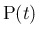 に近い点が
取れることになるので、そのようにしてより近い点を探していけば、
最後にその付近では
に近い点が
取れることになるので、そのようにしてより近い点を探していけば、
最後にその付近では 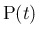 と最も近い
と最も近い 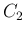 上の点
上の点
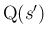 が
取れて、
が
取れて、
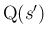 では
では
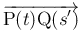 が
が 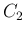 と
垂直になるはずである。この
と
垂直になるはずである。この 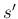 を改めて
を改めて 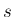 とする (図 9)。
とする (図 9)。
すなわち、
となる (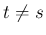 )。一方、前に示したことにより、
)。一方、前に示したことにより、
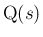 で
で
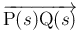 と
と 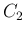 は
垂直なので、
は
垂直なので、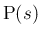 ,
, 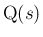 ,
, 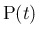 は一直線上に
あることになるが、(10) および
は一直線上に
あることになるが、(10) および
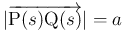 よりその位置関係は、
よりその位置関係は、
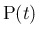 が線分
が線分
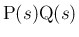 の上にあるか、または
の上にあるか、または
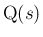 が線分
が線分
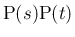 の上にあるかのいずれかとなる。
前者の場合は、
の上にあるかのいずれかとなる。
前者の場合は、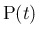 が、
が、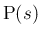 で
で 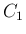 に外接する
半径
に外接する
半径 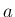 の円の中に含まれてしまうことになるので、
それは曲率に関する仮定 (6) (の下に書いたこと) に
反することになる。
の円の中に含まれてしまうことになるので、
それは曲率に関する仮定 (6) (の下に書いたこと) に
反することになる。
また、後者の場合は、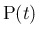 と
と 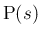 の距離は
の距離は 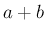 で、
で、
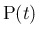 は
は 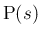 での
での 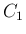 の外向きの法線の上にあることになる。
となればやはり
の外向きの法線の上にあることになる。
となればやはり 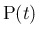 が、
が、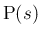 で
で 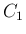 に外接する
半径
に外接する
半径 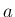 の円の中に含まれてしまうことになるので、
同じ仮定 (6) (の下に書いたこと) に
反することになる。
よってそれらはいずれも起こりえず、
結局
の円の中に含まれてしまうことになるので、
同じ仮定 (6) (の下に書いたこと) に
反することになる。
よってそれらはいずれも起こりえず、
結局 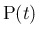 と
と 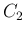 上の点で最短距離にあるのが
上の点で最短距離にあるのが 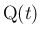 で
あることがわかり、
すなわちすべての点で
で
あることがわかり、
すなわちすべての点で 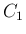 と
と 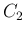 との最短距離が
との最短距離が 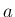 で
あることが示されたことになる。
で
あることが示されたことになる。
竹野茂治@新潟工科大学