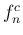 になるだろうか
になるだろうか
今回、以下の疑問に答えるために、もう一つの実験を行った。
管が直管の場合にホルンと同様の演奏を行うと、 自然倍音の周波数は閉管の周波数になるだろうか
金管楽器の自然倍音が、(2) の開管周波数 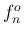 の
ような音になるのは、金管楽器が直管ではなく、
徐々に広がっているから ([1],[3]) という
話があるが、直管と徐々に広がる管に果たしてそんなに違いが出るのだろうかと
まず単純に疑問に感じた。
の
ような音になるのは、金管楽器が直管ではなく、
徐々に広がっているから ([1],[3]) という
話があるが、直管と徐々に広がる管に果たしてそんなに違いが出るのだろうかと
まず単純に疑問に感じた。
また直管の閉管で共鳴周波数が 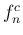 になるというのは、
通常は止まっている気体に対して外から可変な音を鳴らして共鳴する
周波数を探す、という方法で調べるもので、
いわゆる金管楽器の演奏とはだいぶ異なる。
金管楽器は、マウスピースから息を吹きこんで演奏するので、
管内の気体は常に出口に向かって動いていて、よって外側に出る音波と
出口から反射してマウスピース側に戻る音波の速度には違いがあるだろうから、
それが定常波を作って共鳴するための条件は、
止まっている気体の場合とはずれる可能性があるような気がする。
そもそも外から入れた音による共鳴、
例えば金管楽器に向かって「アー」という声を入れた場合と、
管楽器の演奏による共鳴、すなわち唇の振動と連続的な息の投入によるかなり
大きな音による演奏では、エネルギーの強さなどからしても現象自体にかなり
違いがあるような気がするので、共鳴音にも違いがあってもおかしくはない。
になるというのは、
通常は止まっている気体に対して外から可変な音を鳴らして共鳴する
周波数を探す、という方法で調べるもので、
いわゆる金管楽器の演奏とはだいぶ異なる。
金管楽器は、マウスピースから息を吹きこんで演奏するので、
管内の気体は常に出口に向かって動いていて、よって外側に出る音波と
出口から反射してマウスピース側に戻る音波の速度には違いがあるだろうから、
それが定常波を作って共鳴するための条件は、
止まっている気体の場合とはずれる可能性があるような気がする。
そもそも外から入れた音による共鳴、
例えば金管楽器に向かって「アー」という声を入れた場合と、
管楽器の演奏による共鳴、すなわち唇の振動と連続的な息の投入によるかなり
大きな音による演奏では、エネルギーの強さなどからしても現象自体にかなり
違いがあるような気がするので、共鳴音にも違いがあってもおかしくはない。
そこで、実際に直管で、金管楽器同様に演奏して自然倍音を発生させて、 その周波数を調べてみることにした。 直管としては、水道管の蛇口につける、内径 14mm、長さ 4m 強 (4.16m) の 家庭用のホースを使った。F 管のホルンの全長は約 3.7m 位らしいが、 1 番バルブを押すと管長は 45cm 位長くなるようなので、 長さだけみればほぼそれに近い。
そのホースにホルンのマウスピースを刺した状態で、
ホースを巻いた状態でホルンと同じように演奏し、
音が出せる 1 番低い自然倍音 (その 1 次成分を 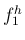 とする) から 16 番目の自然倍音 (1 次成分が
とする) から 16 番目の自然倍音 (1 次成分が 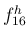 ) までを録音した。
ただし、演奏者は前節のホルンの場合と同じで、技量は高くはない。
音は、各自然倍音で 10 秒程度演奏し、
ほぼホルンの場合と同条件で録音したが、
サイレントブラスやミュートは用いていない。
) までを録音した。
ただし、演奏者は前節のホルンの場合と同じで、技量は高くはない。
音は、各自然倍音で 10 秒程度演奏し、
ほぼホルンの場合と同条件で録音したが、
サイレントブラスやミュートは用いていない。
この場合の、1 番目、8 番目、16 番目の実音の FFT による周波数のグラフを 図 5、図 6 に示す。
ホースの場合も、低い自然倍音には、高次成分がかなり多く含まれるが、 高い自然倍音にはそれらはなくなってくる。
さて、こちらのグラフで示した点線の周波数 (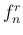 ) は、
ホースの 1 次倍音成分
) は、
ホースの 1 次倍音成分 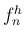 に近くなるよう、
とりあえず 1 番目のグラフでは 50Hz とし、
その後はそれを
に近くなるよう、
とりあえず 1 番目のグラフでは 50Hz とし、
その後はそれを 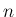 倍したものを書いているが、
明らかに大きい
倍したものを書いているが、
明らかに大きい 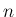 に対しては
に対しては 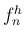 と
と 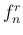 にはずれがある。
すなわち、ホースの自然倍音は、
にはずれがある。
すなわち、ホースの自然倍音は、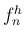 は開管 (2) の
形とは違っていることが予想される。
実際、今回のデータから得た
は開管 (2) の
形とは違っていることが予想される。
実際、今回のデータから得た 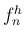 は表 3 のようになる。
なお、3 列目、5 列目は
は表 3 のようになる。
なお、3 列目、5 列目は
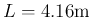 の管長から理論的に計算される
共鳴周波数の値
の管長から理論的に計算される
共鳴周波数の値
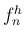 とそれらとの単純差を計算したものである。
ここで、閉管 (1)、開管 (2) の
とそれらとの単純差を計算したものである。
ここで、閉管 (1)、開管 (2) の 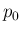 はいずれも、気温 18
はいずれも、気温 18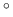 C 位の音速
C 位の音速
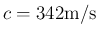 と
管長
と
管長
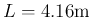 に対して、
となる。なお、
に対して、
となる。なお、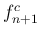 と
と 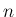 を一つ増やしている理由は後述する。
を一つ増やしている理由は後述する。
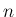 で
で
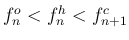 となっていること、
および
となっていること、
および 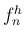 の値は、そのどちらに近いとも言えないことがわかる。
の値は、そのどちらに近いとも言えないことがわかる。
さて、
ホルンの自然倍音の 1 次成分の周波数 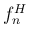 と、
ホースの自然倍音の 1 次成分の周波数
と、
ホースの自然倍音の 1 次成分の周波数 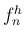 を
グラフにしたものが図 7 である。
を
グラフにしたものが図 7 である。
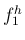 は
は 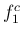 ではなく
ではなく 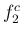 の実音であり、
の実音であり、
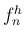 はむしろ
はむしろ 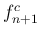 に対応する、というように見える。
に対応する、というように見える。
ホルンの実音とホースの実音が、閉管形の式 (1)、
あるいは開管形の式 (2) のいずれに対応するのかを
見るために、それぞれの相関係数や回帰直線を計算すると、
その結果は表 4 のようになり、図 7 に
描かれている直線がそれぞれの回帰直線である。
見てわかるように、相関係数は非常に 1 に近く、 ほぼ直線になっていることがわかり、よって回帰直線の信頼度もかなり高い。
ホルンの回帰直線は、定数項はあるもののある程度小さく、
傾きの 13% 程度であるが、ホースの方は傾きの 32% 程度の数値なので
無視できる値ではなく、0 よりもむしろ 0.5 に近い。
つまり、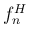 の方は
の方は 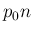 という式にある程度近いが、
という式にある程度近いが、
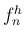 の方はどちらかといえば
の方はどちらかといえば 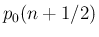 に近い形になっている。
に近い形になっている。
ただ、0.322 がもっと 0.5 に近ければ、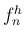 は閉管 (1) 形で、
は閉管 (1) 形で、
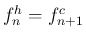 と一つずれた形であることがはっきりするのだが、
18% も違いがあるとそこまで明確には述べられない。
一方で、この回帰直線の
と一つずれた形であることがはっきりするのだが、
18% も違いがあるとそこまで明確には述べられない。
一方で、この回帰直線の 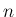 の係数である 41.0Hz は、(11) の
の係数である 41.0Hz は、(11) の
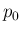 の値によく対応していて、
よって 0.322 と 0.5 のずれは、誤差というよりも、
何らかの理由により起きている差だと感じられる。
の値によく対応していて、
よって 0.322 と 0.5 のずれは、誤差というよりも、
何らかの理由により起きている差だと感じられる。
とりあえず、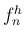 には、今回は出せなかったが多分
には、今回は出せなかったが多分 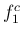 に
対応する
に
対応する 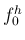 の一番低い音があって、よってそこから数えると
ホースの自然倍音は
の一番低い音があって、よってそこから数えると
ホースの自然倍音は
この 18% 位ずれている部分が、もしかしたら本節の始めに述べた、 止まっている空気の閉管と流れている空気の演奏の違いや、 共鳴現象自体の違いによるものなのかもしれないが、 詳しいことはわからない。
また、ホルンの方も 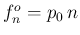 の形にある程度近い、とはいうものの、
13% 程度のずれがあることは完全に無視できるような値ではない。
しかし、これも今回使用した楽器の癖や演奏者の技量による影響なのか、
楽器の構造上完全に
の形にある程度近い、とはいうものの、
13% 程度のずれがあることは完全に無視できるような値ではない。
しかし、これも今回使用した楽器の癖や演奏者の技量による影響なのか、
楽器の構造上完全に 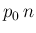 に一致しないことの影響なのかはわからない。
に一致しないことの影響なのかはわからない。
例えば、やや苦しそうな 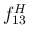 の音を除くと、
回帰直線は
の音を除くと、
回帰直線は
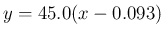 と 9% 位のやや小さいずれになるので、
技量による要因も小さくない気がする。
と 9% 位のやや小さいずれになるので、
技量による要因も小さくない気がする。
竹野茂治@新潟工科大学