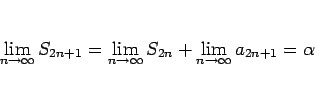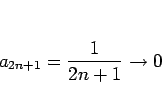次へ: 3 級数の間の等式
上へ: ある無限級数の値について
前へ: 1 はじめに
(PDF ファイル: series1.pdf)
2 補題
考える級数 (1) の部分和
の極限を考えればよいが、まず次の補題を示す。
補題 1
無限級数
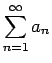 の部分和
の部分和
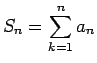 について、
について、
ならば、この無限級数は収束し
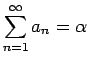 となる。
となる。
証明
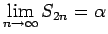 であるし、
であるし、
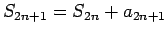 より、仮定から
より、仮定から
なので、よって
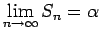 となる。
となる。
この無限級数 (1) に対しても、明らかに
なので、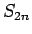 の極限を考えればよい。
の極限を考えればよい。
次へ: 3 級数の間の等式
上へ: ある無限級数の値について
前へ: 1 はじめに
竹野茂治@新潟工科大学
2006年4月25日
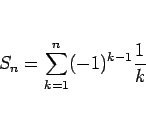
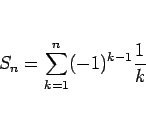
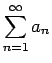 の部分和
の部分和
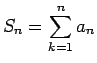 について、
について、
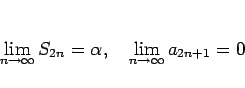
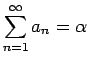 となる。
となる。
![]() であるし、
であるし、
![]() より、仮定から
より、仮定から