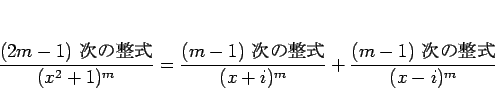次へ: 2 共役による対称性
上へ: 複素数を利用した有理関数の積分
前へ: 複素数を利用した有理関数の積分
(PDF ファイル: quotef4.pdf)
1 はじめに
[1] では、有理関数の積分の難点である
の積分を、分子が奇数次と偶数次の項に分離し、その偶数次の方に対しては
部分積分を使って計算する方法について、
また、[2] では、それを未定係数法で計算する方法について
考察した。
複素数を使えば、
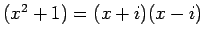 のように因数分解されるから、
容易に想像されるように、これには、複素数を用いて、
のように因数分解されるから、
容易に想像されるように、これには、複素数を用いて、
のように部分分数分解をしてから計算する方法もある。
しかし、実際に計算してみればわかるが、それはそれほど簡単ではない。
共役複素数を利用してその対称性を使えば、多少楽にはできるのではあるが、
それでも部分積分等の方法に代わる、というほどの方法ではない。
ここでは、その対称性等の性質を具体例を含めてまとめておく。
次へ: 2 共役による対称性
上へ: 複素数を利用した有理関数の積分
前へ: 複素数を利用した有理関数の積分
竹野茂治@新潟工科大学
2006年6月2日
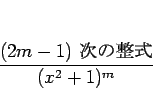
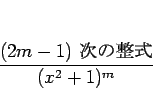
![]() のように因数分解されるから、
容易に想像されるように、これには、複素数を用いて、
のように因数分解されるから、
容易に想像されるように、これには、複素数を用いて、