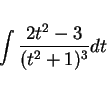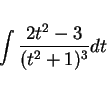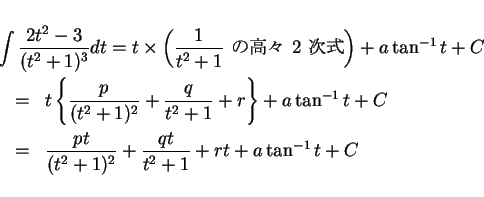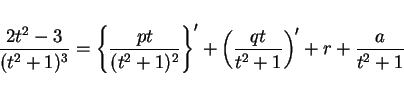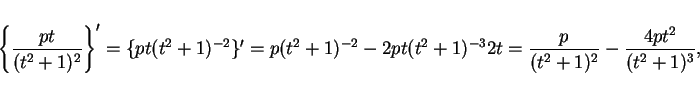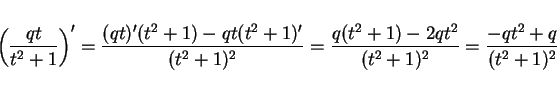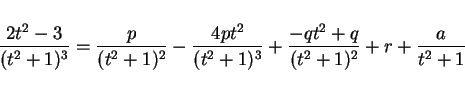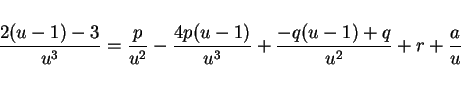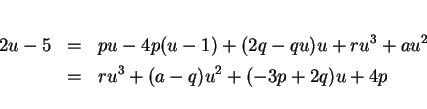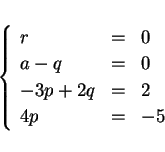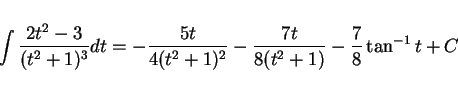

Next: 4.3 部分積分で次数を落とす方法
Up: 4 分子が偶数次の項の場合
Previous: 4.1 t=tanθと置換する方法
(PDF ファイル: quotef1.pdf)
4.1 節の結果である (3) を利用して、
未定係数法でこの積分を求める、という方法もある。
例 2
積分
を未定係数法で求める。
4.1 節の結果 (3) により、
とする (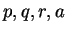 は未定係数)。ただし (3)
を導き出す過程を詳しく見るとわかるが、
実際には
は未定係数)。ただし (3)
を導き出す過程を詳しく見るとわかるが、
実際には 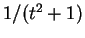 の 2 次式の定数項
の 2 次式の定数項 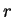 は不要である。
は不要である。
この式の両辺を微分する。
であり、
なので、よって
となる。簡単のため、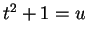 , すなわち
, すなわち 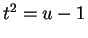 とすると、
とすると、
となり、両辺 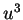 倍すると
倍すると
となる。よって係数比較すれば
の連立方程式を得、これを解いて 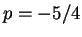 ,
, 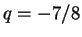 ,
, 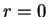 ,
, 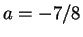 を得る。
ゆえに
を得る。
ゆえに
である。


Next: 4.3 部分積分で次数を落とす方法
Up: 4 分子が偶数次の項の場合
Previous: 4.1 t=tanθと置換する方法
Shigeharu TAKENO
2003年 5月 26日