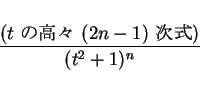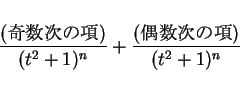

Next: 3 分子が奇数次の項の場合
Up: 有理関数の積分について
Previous: 1 有理関数の積分
(PDF ファイル: quotef1.pdf)
有理関数の分母にある (実数係数の) 多項式は、代数学の基本定理により
1 次式、および実数の範囲では因数分解できない 2 次式の積で因数分解
できることが保証されるので、一般の有理関数は部分分数分解を行えば
のような形のものの和に分解されることになる。
多項式の積分は容易、2 番目の形のものも 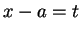 と置換すれば
と置換すれば
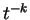 (
(
 ) の形の項の和になり、
これも容易に積分できる。
) の形の項の和になり、
これも容易に積分できる。
問題は最後の形のものであるが、これは 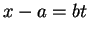 と置換することで
と置換することで
となり、これを
の二つに分けて考えることにする。


Next: 3 分子が奇数次の項の場合
Up: 有理関数の積分について
Previous: 1 有理関数の積分
Shigeharu TAKENO
2003年 5月 26日
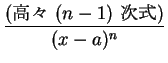 (
(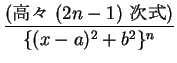 (
(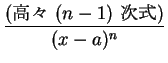 (
(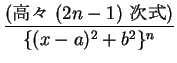 (
(![]() と置換すれば
と置換すれば
![]() (
(
![]() ) の形の項の和になり、
これも容易に積分できる。
) の形の項の和になり、
これも容易に積分できる。
![]() と置換することで
と置換することで