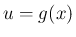 が
が 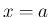 で微分可能、すなわち
で微分可能、すなわち
が
で微分可能、すなわち
の極限値が存在し、が
で微分可能、すなわち
の極限値が存在するとき、合成関数は
で微分可能で、 その微分係数
は
となる。まず、この公式の、高校の教科書などに書かれている証明を改めて紹介する。
証明
であり、とすれば
で、 また仮定 (1) より
となるので、(4) は、
と書ける。よって、(5), および仮定 (1), (2) により (7) はの ときに
に収束するので (3) が成り立つ。
(証明おわり)
高校の教科書などの証明はこれで終わりなのであるが、 講義の教科書 [1] の付録にある証明で指摘している通り、 上の証明には問題がある。それは、(6) の式変形の部分である。 元々、
の定義は、「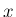 が
が 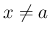 の状態を保ちながら
の状態を保ちながら 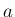 に近づくとき、
それはどのような近づきかたをしても
に近づくとき、
それはどのような近づきかたをしても 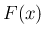 の値が
の値が 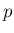 に近づくこと」
であり、特定の点列を除外して近づくことは許されない。
に近づくこと」
であり、特定の点列を除外して近づくことは許されない。
一方で、
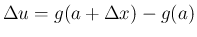 は、
は、
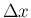 が 0 に近づくときに途中で
が 0 に近づくときに途中で 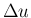 が 0 の値を取ることは
十分ありうるし、それが無限個の場合もありうる。その簡単な例は、
が 0 の値を取ることは
十分ありうるし、それが無限個の場合もありうる。その簡単な例は、
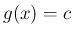 (定数) の場合であり、
教科書 [1] に書いてあるような
(定数) の場合であり、
教科書 [1] に書いてあるような 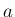 の近くで無限に振動する場合もある。
ところが
の近くで無限に振動する場合もある。
ところが 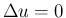 となる
となる 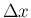 では
当然 (6) の式変形が行えず、
よってそのような
では
当然 (6) の式変形が行えず、
よってそのような 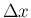 に対しては (6), (7) では
に対しては (6), (7) では 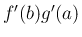 に
収束することが示せていない、ということが問題となる。
に
収束することが示せていない、ということが問題となる。
これを、場合分けして考えるのが教科書の付録にある証明であるが、
少しそれを明確にするために次のような集合を導入しよう。
十分小さい 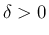 に対して、集合
に対して、集合 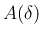 ,
, 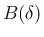 を
を
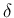 に対して
に対して 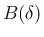 が空集合になれば、
が空集合になれば、
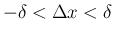 ,
,
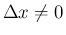 に対して、
に対して、
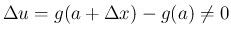 なので上の論法で証明は終了する。
なので上の論法で証明は終了する。
問題なのは、どんなに小さい 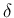 に対しても
に対しても 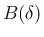 が空集合に
ならない場合、すなわち
が空集合に
ならない場合、すなわち 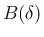 の中に少なくとも 0 に収束するような
の中に少なくとも 0 に収束するような 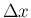 の無限列が存在する場合である。以下、そのような場合を考える。
の無限列が存在する場合である。以下、そのような場合を考える。
この場合、逆に 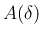 が空になる場合もあるが、
が空になる場合もあるが、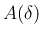 内で
0 に収束するような
内で
0 に収束するような 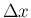 の列に対しては、上の論法により
(4) が
の列に対しては、上の論法により
(4) が 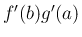 に収束することは言える。
に収束することは言える。
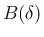 内で 0 に収束するような
内で 0 に収束するような 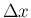 の列を
の列を
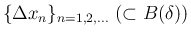 と
書くことにすると、
と
書くことにすると、
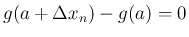 であり、
よって
であり、
よって
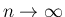 に対して、仮定 (1) により
に対して、仮定 (1) により
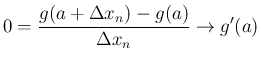
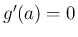 でなければいけないことになる。
そして、当然
でなければいけないことになる。
そして、当然
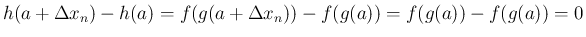
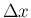 がどのように近づいても (4) は 0 に収束することになり、
すなわちその極限の存在が保証され、
まず
がどのように近づいても (4) は 0 に収束することになり、
すなわちその極限の存在が保証され、
まず 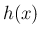 が
が 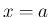 で微分可能であることがわかる。
そして、その微分係数
で微分可能であることがわかる。
そして、その微分係数 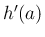 は 0 であり、
それは確かに
は 0 であり、
それは確かに 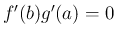 に一致することになる。
に一致することになる。
これで、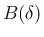 の中に少なくとも 0 に収束するような
の中に少なくとも 0 に収束するような 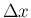 の無限列が存在する場合でも、
公式 2.6 が成り立つことが示されたことになる。
の無限列が存在する場合でも、
公式 2.6 が成り立つことが示されたことになる。
教科書 [1] 付録の証明も、ほぼ同じことを言っているのであるが、 若干説明が足りないので、やや理解しにくいのではないかと思う。
竹野茂治@新潟工科大学