3 逆関数の関係を利用する証明
前節で述べた証明の他に、逆関数の関係
を利用して、一方から他方、すなわち指数関数の微分から対数関数の微分、
または対数関数の微分から指数関数の微分を導く方法もある。
これは、一般には逆関数の微分法 (教科書 [1] では公式 2.17) を
使うのだが、逆関数の微分法は、
対数微分法と同様に合成関数の微分の応用と見ることができるので、
合成関数の微分法のみで示すことも可能である。
本節では、その考え方で、一方から他方を導く証明を考えてみる。
まずは、公式 1 を仮定して公式 2 を導いてみる。
すなわち
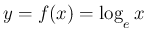 の導関数を求める。
これは、
の導関数を求める。
これは、
と書けるので、この式の両辺を 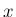 で微分すると、左辺の微分は 1 で、
右辺の微分は、公式 1 と合成関数の微分により、
となるから、
で微分すると、左辺の微分は 1 で、
右辺の微分は、公式 1 と合成関数の微分により、
となるから、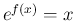 より
より
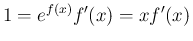 となり、よって
となり公式 2 が得られた。
となり、よって
となり公式 2 が得られた。
今度は、公式 4 を仮定して公式 3、すなわち 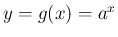 の
導関数を求める。これは、
の
導関数を求める。これは、
と書け、両辺を 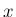 で微分すると公式 4 と合成関数の微分により、
となるので、
で微分すると公式 4 と合成関数の微分により、
となるので、
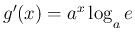 の公式 3 が得られる。
の公式 3 が得られる。
竹野茂治@新潟工科大学
2022-11-01
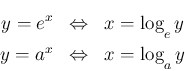
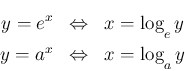
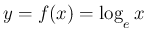 の導関数を求める。
これは、
の導関数を求める。
これは、
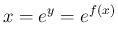
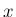 で微分すると、左辺の微分は 1 で、
右辺の微分は、公式 1 と合成関数の微分により、
で微分すると、左辺の微分は 1 で、
右辺の微分は、公式 1 と合成関数の微分により、
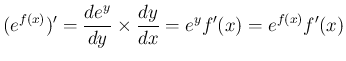
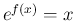 より
より
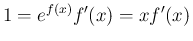 となり、よって
となり、よって
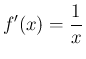
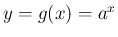 の
導関数を求める。これは、
の
導関数を求める。これは、
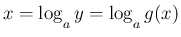
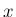 で微分すると公式 4 と合成関数の微分により、
で微分すると公式 4 と合成関数の微分により、
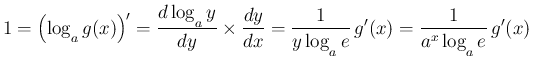
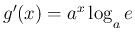 の公式 3 が得られる。
の公式 3 が得られる。