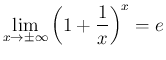 (1)
(1)
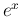 、対数関数
、対数関数
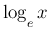 の導関数を決定する大事な
極限であるが、教科書[1] ではその証明を省略しているので、
本稿ではそれを紹介する。証明の元になるのは、
の導関数を決定する大事な
極限であるが、教科書[1] ではその証明を省略しているので、
本稿ではそれを紹介する。証明の元になるのは、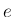 の定義
である。
なお、(2) は
の定義
である。
なお、(2) は 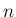 で書いてあるから
この
で書いてあるから
この 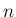 は自然数を意味し、
(1) は
は自然数を意味し、
(1) は 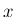 で書いてあるからこの
で書いてあるからこの 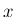 は
実数を意味することに注意しよう。
つまり、(1) の極限は、
は
実数を意味することに注意しよう。
つまり、(1) の極限は、
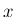 は整数以外の値も取りながらの極限を意味する。
は整数以外の値も取りながらの極限を意味する。
また、(1) で「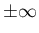 」となっているのは、
」となっているのは、
ちなみにこの (1) は、最終的には [1] p13 の 上にある
を示すためのものである。もし (1)、すなわち (3) と (4) が言えれば、 (3) で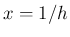 (
(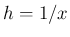 ) と
すると
) と
すると
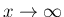 は
は
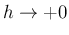 を意味し、よって
が得られ、(4) で
を意味し、よって
が得られ、(4) で 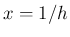 (
(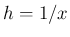 ) と
すると
) と
すると
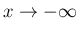 は
は
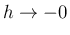 を意味し、よって
が得られるので、よって (6), (7) の両方を合わせて (5) が得られることになる。
を意味し、よって
が得られるので、よって (6), (7) の両方を合わせて (5) が得られることになる。
最初の定義 (2) で 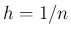 としても、それは 1/2,1/3,1/4,...
というとびとびの
としても、それは 1/2,1/3,1/4,...
というとびとびの 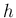 の値に対してのみ
の値に対してのみ 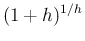 の極限が
の極限が 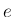 になる、
ということしか言えたことにはならず、
(5) はおろか (6) にすらならない。
だから、(5) を示すためには、定義 (2) の
になる、
ということしか言えたことにはならず、
(5) はおろか (6) にすらならない。
だから、(5) を示すためには、定義 (2) の 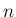 を
実数
を
実数 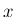 に拡張したもの (3)、および
負の無限大の方向の極限 (4) も同じ値になること、
すなわち (1) が必要になるのである。
に拡張したもの (3)、および
負の無限大の方向の極限 (4) も同じ値になること、
すなわち (1) が必要になるのである。
竹野茂治@新潟工科大学