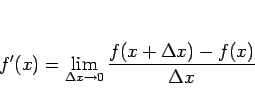2 極限による通常の定義
現在、導関数の定義は、極限を用いて、
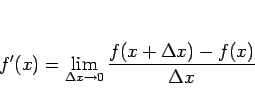 |
(1) |
のように行われる。
しかし、それによって通常行われる積の微分、商の微分の証明は、
やや見通しが悪いように思う。
例えば積の微分は、通常以下のように行われる。
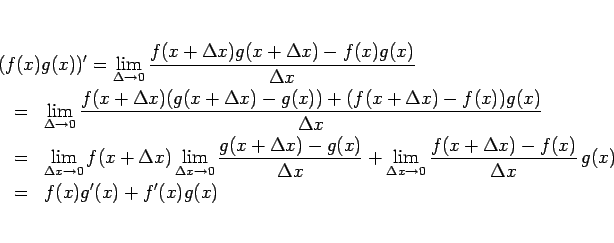
この途中の変形は、やや不自然に見えて、あまりわかりやすい証明とは
言えないと感じるが、以下のようにすると多少は改善すると思う。
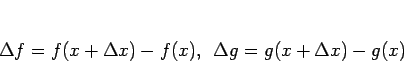
とすると、
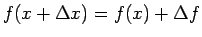 ,
,
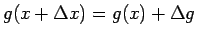 で、
で、
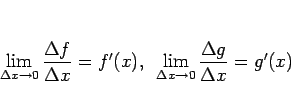
より、
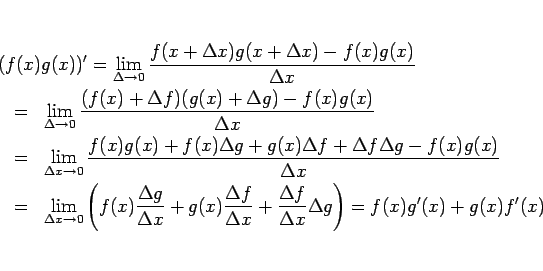
となる、というやり方である。
これなら、途中の計算は自然に展開するだけなので、
よりわかりやすいだろうと思う。
実は、この方法は「無限小」による証明に近い手法である。
竹野茂治@新潟工科大学
2015年12月7日