6 5 次、6 次の計算方法
最後に、4 節、5 節で得られた結果を用いて、
5 次, 6 次の行列式の計算方法を紹介する。
まずは 5 次を考えると、5 は 4 で割って 1 余るので、
一つの面に対する斜めの積につける順列の符号はすべて 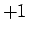 となる:
となる:
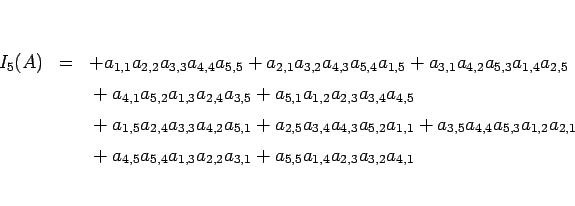
一方、
![\begin{displaymath}
C_5=\{p(0,i,j,0)=[2,3,4,5]^{(j)}\circ [3,4,5]^{(i)}; 0\leq j<4, 0\leq i<3\}
\end{displaymath}](img252.gif)
であるので、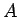 を
を 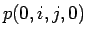 に対応した行の入れ換え、
すなわち、下 3 行を
に対応した行の入れ換え、
すなわち、下 3 行を 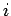 回巡回し、その後で下 4 行を
回巡回し、その後で下 4 行を 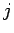 回巡回したものを
回巡回したものを
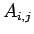 と書くことにすると、
と書くことにすると、
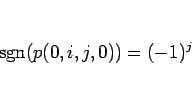
なので、
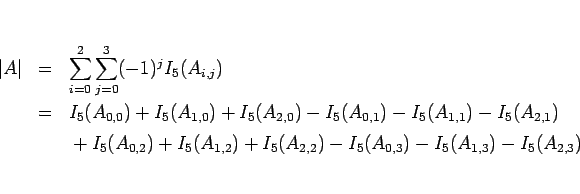
となる。つまり、下 3 行の巡回では符号は変えずに、
下 4 行の巡回のときに 1 回ずつ符号を変えて加えればよい。
次に 6 次の場合を考える。
6 は 4 で割って 2 余るので、
一つの面に対する斜めの積につける順列の符号は、
左上から右下への対角線の積には 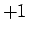 、
右上から左下への対角線の積には
、
右上から左下への対角線の積には 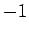 をつけ、
その下には
をつけ、
その下には 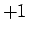 と
と 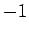 を交互につける。
を交互につける。

一方、
![\begin{displaymath}
p(0,i,j,k,0)=[2,3,4,5,6]^{(k)}\circ [3,4,5,6]^{(j)}\circ [4,5,6]^{(i)}
\end{displaymath}](img258.gif)
に対応して行を巡回した 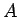 を
を 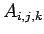 と書くことにすると、
と書くことにすると、
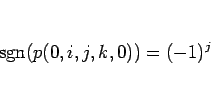
なので、

となる。つまり、下 3 行の巡回、下 5 行の巡回では符号は変えずに、
下 4 行の巡回のときに 1 回ずつ符号を変えて加えればよい。
竹野茂治@新潟工科大学
2008年7月26日
![]() となる:
となる:
![]() 、
右上から左下への対角線の積には
、
右上から左下への対角線の積には ![]() をつけ、
その下には
をつけ、
その下には ![]() と
と ![]() を交互につける。
を交互につける。