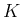 を実数全体の集合 (通常
を実数全体の集合 (通常 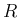 と書く)、
または複素数全体の集合 (通常
と書く)、
または複素数全体の集合 (通常 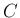 と書く) のいずれかとするが、
と書く) のいずれかとするが、
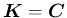 と考えてもらってさしつかえない。
と考えてもらってさしつかえない。
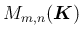 を
を 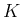 の元を要素とする
の元を要素とする 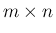 行列全体の集合とし、
行列全体の集合とし、
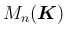 を
を 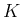 の元を要素とする
の元を要素とする 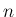 次正方行列全体の集合とする。
次正方行列全体の集合とする。
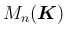 に内積とそこから自然に決まる長さ (ノルム) を導入する。
に内積とそこから自然に決まる長さ (ノルム) を導入する。
![$A=[a_{ij}]_{i,j}\in M_n(\mbox{\boldmath$K$})$](img12.png) ,
,
![$B=[b_{ij}]_{i,j}\in M_n(\mbox{\boldmath$K$})$](img13.png) の
内積
の
内積 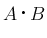 を
を
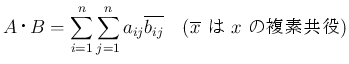
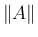 を、
を、
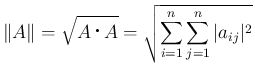
 を実数全体の集合 (通常
を実数全体の集合 (通常 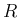 と書く)、
または複素数全体の集合 (通常
と書く)、
または複素数全体の集合 (通常 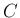 と書く) のいずれかとするが、
と書く) のいずれかとするが、
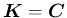 と考えてもらってさしつかえない。
と考えてもらってさしつかえない。
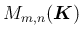 を
を 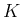 の元を要素とする
の元を要素とする 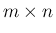 行列全体の集合とし、
行列全体の集合とし、
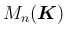 を
を 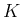 の元を要素とする
の元を要素とする 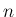 次正方行列全体の集合とする。
次正方行列全体の集合とする。
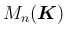 に内積とそこから自然に決まる長さ (ノルム) を導入する。
に内積とそこから自然に決まる長さ (ノルム) を導入する。
![$A=[a_{ij}]_{i,j}\in M_n(\mbox{\boldmath$K$})$](img12.png) ,
,
![$B=[b_{ij}]_{i,j}\in M_n(\mbox{\boldmath$K$})$](img13.png) の
内積
の
内積 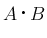 を
を
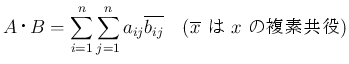
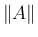 を、
を、
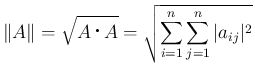
長さは以下を満たす。
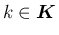 ,
,
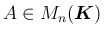 ならば
ならば
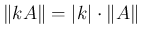
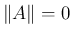 と
と 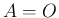 は同値
は同値
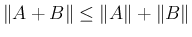
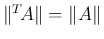
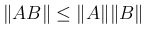
1., 2., 3. は通常の  次元ベクトルの場合と同じだから省略。
4. も明らか。最後の 5. のみ示す。
次元ベクトルの場合と同じだから省略。
4. も明らか。最後の 5. のみ示す。
![$A=[a_{ij}]_{i,j}$](img26.png) ,
,
![$B=[b_{ij}]_{i,j}$](img27.png) ,
,
![$C=AB=[c_{ij}]_{i,j}$](img28.png) とすると、
とすると、
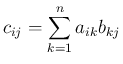
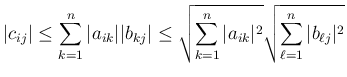
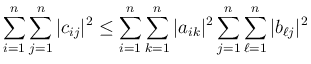
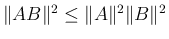 が得られる。
が得られる。
 (
(
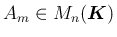 ) の
極限
) の
極限
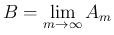 を、
を、
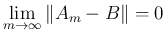
![$A_m=[a_{ij}(m)]_{i,j}$](img37.png) ,
,
![$B=[b_{ij}]_{i,j}$](img27.png) と
書けば、容易に
と
書けば、容易に
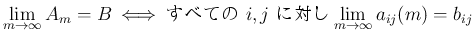
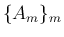 (
(
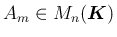 ) が コーシー列 であるとは、
) が コーシー列 であるとは、
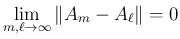
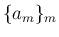 の場合、
の場合、
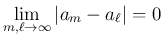
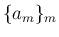 がコーシー列であることと、
それがある有限な極限値
がコーシー列であることと、
それがある有限な極限値 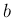 に収束することは同値となる (証明は省略、実数論と関係する)。
そして、行列の無限列に対しても同じことが言える。
に収束することは同値となる (証明は省略、実数論と関係する)。
そして、行列の無限列に対しても同じことが言える。
行列の無限列証明(
) がコーシー列であることと、 ある行列
に収束することは同値。
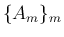 が
が 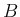 に収束すれば、
に収束すれば、
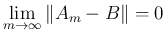
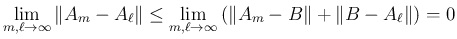
逆に、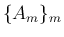 がコーシー列であれば、
がコーシー列であれば、
![$A_m=[a_{ij}(m)]_{i,j}$](img37.png) の成分も、
の成分も、
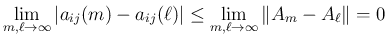
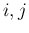 に対してコーシー列となり、
よってそれぞれ極限
に対してコーシー列となり、
よってそれぞれ極限 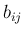 が存在する。
よって
が存在する。
よって
![$A_m=[a_{ij}(m)]_{i,j}$](img37.png) は
は
![$B=[b_{ij}]_{i,j}$](img27.png) に収束する。
に収束する。
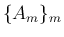 (
(
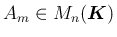 ) に対する 無限級数
) に対する 無限級数
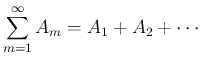
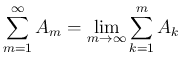
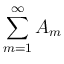 は、
すべての
は、
すべての 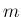 に対し
に対し
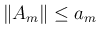 で、
で、
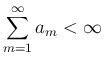 となる非負実数列
となる非負実数列 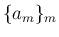 が
存在するとき、絶対収束する といい、
が
存在するとき、絶対収束する といい、
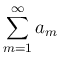 を
を
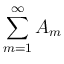 の 優級数 と呼ぶ。
の 優級数 と呼ぶ。
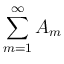 は収束する。
は収束する。
証明
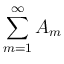 の部分和
の部分和
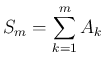 が
コーシー列であることを示せばよい。
が
コーシー列であることを示せばよい。
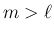 に対して、
に対して、
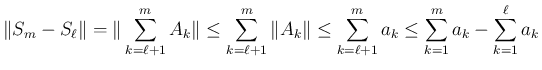
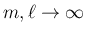 のときに 0 に収束するので、左辺はコーシー列となる。
のときに 0 に収束するので、左辺はコーシー列となる。
竹野茂治@新潟工科大学