

Next: この文書について...
Up: テイラー展開 その 2
Previous: 2 計算方法
(PDF ファイル: taylor3.pdf)
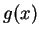 のマクローリン展開であるが、
のマクローリン展開であるが、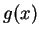 は
は 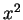 の関数なので、
の関数なので、
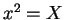 として
として
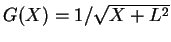 の
の 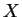 に関する
マクローリン展開を求めて、その式に
に関する
マクローリン展開を求めて、その式に 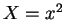 を代入すればいい。
例えば
を代入すればいい。
例えば
だったとすれば、
となるわけである。また、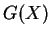 であるが、
であるが、
となるので、この 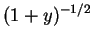 のマクローリン展開に
のマクローリン展開に 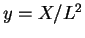 を
代入して
を
代入して 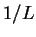 倍すればそれでいい。
倍すればそれでいい。
これらの操作はいずれも、巾級数 (マクローリン展開) の一意性定理により
保証される。
結局、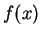 のマクローリン展開は
のマクローリン展開は 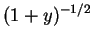 の
の 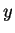 に関する
マクローリン展開に帰着されるわけであるが、
これは最初に上げた一般二項定理 (1) により、
に関する
マクローリン展開に帰着されるわけであるが、
これは最初に上げた一般二項定理 (1) により、
となるので、後はこれを使って
と、順に求まっていくことになる。
4 次以上の項も求めたい場合は
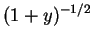 の展開を必要なだけ追加していけば良い。
の展開を必要なだけ追加していけば良い。


Next: この文書について...
Up: テイラー展開 その 2
Previous: 2 計算方法
Shigeharu TAKENO
2003年 11月 27日
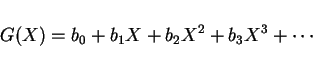
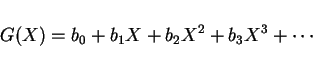
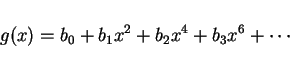
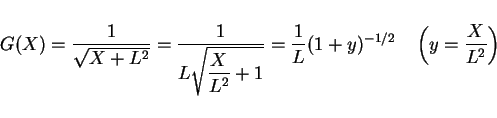
![]() のマクローリン展開は
のマクローリン展開は ![]() の
の ![]() に関する
マクローリン展開に帰着されるわけであるが、
これは最初に上げた一般二項定理 (1) により、
に関する
マクローリン展開に帰着されるわけであるが、
これは最初に上げた一般二項定理 (1) により、
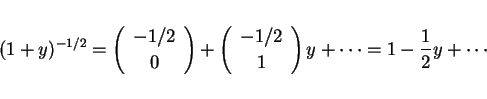
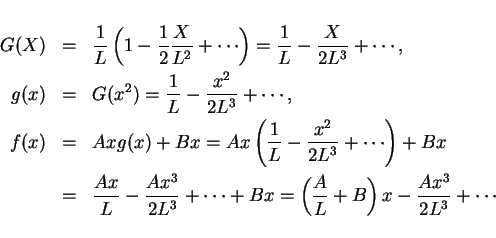
![]() の展開を必要なだけ追加していけば良い。
の展開を必要なだけ追加していけば良い。