6 複素数乗
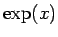 の定義式 (3) の発展として、
最後に「複素数乗」を考えてみる。
(3) の定義は単に自然数乗しか使わないので、
この式の
の定義式 (3) の発展として、
最後に「複素数乗」を考えてみる。
(3) の定義は単に自然数乗しか使わないので、
この式の 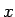 を複素数にしても問題はない。
それにより、いわゆるオイラーの公式による複素数乗が
得られるのかを考えてみる。
を複素数にしても問題はない。
それにより、いわゆるオイラーの公式による複素数乗が
得られるのかを考えてみる。
なお、その考察のために、まず複素数列の収束性を定義し、
複素数の極形式、ド・モアブルの公式を復習しておく。
さて、まず (3) の右辺の 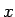 を
を 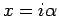 (
(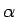 は実数) とした式の極限を考える。
は実数) とした式の極限を考える。
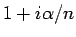 を極形式で表すと、
を極形式で表すと、
となる。ここで、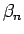 は
は
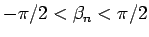 と取れ、
と取れ、
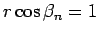 ,
,
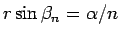 より、
より、
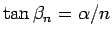 であることに注意する。
ド・モアブルの公式より、
であることに注意する。
ド・モアブルの公式より、
となるが、先頭の根号の中身は命題 4 により、
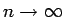 のときに 1 に収束する。
一方、
のときに 1 に収束する。
一方、
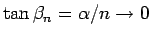 であるから
であるから
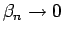 であり、よく知られているように
であり、よく知られているように
であるから、
となることがわかる。よって、 の極限は、
の極限は、
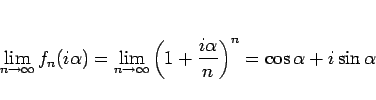 |
(37) |
となるから、これにより 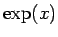 を (3) によって
複素数に拡張すると、
を (3) によって
複素数に拡張すると、
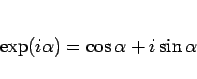 |
(38) |
が成り立つことになる。これは、いわゆるオイラーの公式
「
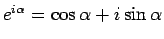 」に対応する。
」に対応する。
さらに 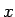 を一般の複素数
を一般の複素数 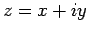 (
(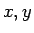 は実数) とすると、
は実数) とすると、
となり、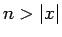 である
である 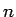 を考えれば
を考えれば 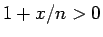 なので、
なので、
より、
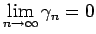 で
で
となることがわかる。
一方、
であり、これは命題 4 により、
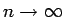 のときに
のときに
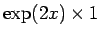 に収束する。
よって、
に収束する。
よって、
となることが (24) からわかる。これは、
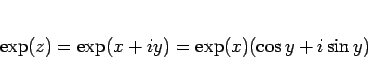 |
(39) |
を意味し、これも通常の 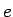 の複素数乗の式に対応する。
の複素数乗の式に対応する。
そして、(39) を用いれば、複素数に対する指数法則
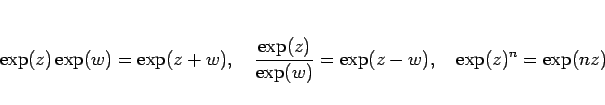 |
(40) |
(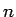 は自然数) も容易に示される。
は自然数) も容易に示される。
竹野茂治@新潟工科大学
2017年2月2日
![]() を一般の複素数
を一般の複素数 ![]() (
(![]() は実数) とすると、
は実数) とすると、