 |
(1) | ||
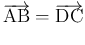 |
(2) | ||
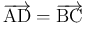 |
(3) |
四角形 ABCD に対して、
演習問題では、 (1) と「(2) かつ (3)」が同値、 としている解答もあったが、 それは、命題として間違ってはいないが、過剰である。 つまり、「(2) かつ (3)」は 「(2) だけ」と同値であり、 「(3) だけ」とも同値となる。
なお、「(2) ならば (3)」、 あるいは「(3) ならば (2)」は、 以下のように代数的に直接得ることもできる。
(2) が成立すると、より、
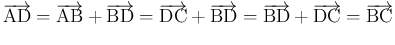
となる。「(3) ならば (2)」も同様である。
さらに、(1) と、
が同値であるとして、それで解こうとしている答案もあった。 (4) は、ほぼ平行四辺形の定義なので 当然 (1) とは同値だが、 (4) を使うために数式にすると、 (2) よりも面倒になり (パラメータが増える)、 (2) を用いる方が易しい。なお、「(2) と (4) が同値」であることは、 以下のようにして直接示すこともできる。 まず、「(2) ならば (4)」の方は、 「(2) ならば (3)」が得られているので、 (2) と (3) の両方が成立することになり、 当然 (4) が成立することになる。
次は「(4) ならば (2)」の方を考える。 ABCD は四角形なので、
と仮定してよい。(4) より、
となるスカラー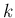 ,
, 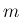 が存在する。よって、
が存在する。よって、
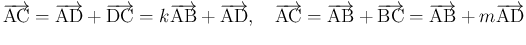
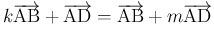
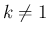 なら、ここから
なら、ここから
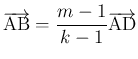
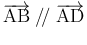 ということになり、
(5) に反する。よって
ということになり、
(5) に反する。よって 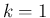 となる。
ついでに言えば、
となる。
ついでに言えば、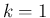 と (7) より
と (7) より
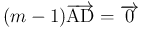 と
なるので、(5) より
と
なるので、(5) より 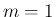 も得られる。
も得られる。
よって、(6) より
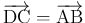 (および
(および
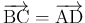 ) となり、
(2) (および (3) が得られることになる。
) となり、
(2) (および (3) が得られることになる。
竹野茂治@新潟工科大学