


Next: 10.2 Operators
Up: 10 Expressions
Previous: 10 Expressions
gnuplot の関数は、Unix 数学ライブラリの関数とほぼ同じですが、特に注
意がなければ全ての関数が整数、実数、複素数の引数を取ることができます。
度、あるいはラジアンのどちらかで角度を引数としたり戻り値としたりする関
数 (sin(x), cos(x), tan(x), asin(x), acos(x), atan(x), atan2(x), arg(z))
に対しては、その単位は set angles で選択でき、デフォルトはラジアンで
す。
| 数学ライブラリ関数 |
| 関数 |
引数 |
戻り値 |
| abs(x) |
任意 |
 の絶対値, の絶対値, 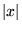 ; 同じ型 ; 同じ型 |
| abs(x) |
複素数 |
 の長さ, の長さ,
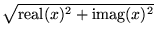 |
| acos(x) |
任意 |
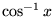 (アークコサイン) (アークコサイン) |
| acosh(x) |
任意 |
ラジアンでの 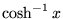 (逆双曲余弦) (逆双曲余弦) |
| arg(x) |
複素数 |
 の偏角 の偏角 |
| asin(x) |
任意 |
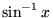 (アークサイン) (アークサイン) |
| asinh(x) |
任意 |
ラジアンでの 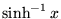 (逆双曲正弦) (逆双曲正弦) |
| atan(x) |
任意 |
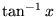 (アークタンジェント) (アークタンジェント) |
| atan2(y,x) |
整数または実数 |
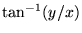 (アークタンジェント) (アークタンジェント) |
| atanh(x) |
任意 |
ラジアンでの 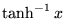 (逆双曲正接) (逆双曲正接) |
| besj0(x) |
整数または実数 |
 の の 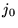 次ベッセル関数 次ベッセル関数 |
| besj1(x) |
整数または実数 |
 の の 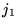 次ベッセル関数 次ベッセル関数 |
| besy0(x) |
整数または実数 |
 の の 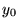 次ベッセル関数 次ベッセル関数 |
| besy1(x) |
整数または実数 |
 の の 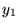 次ベッセル関数 次ベッセル関数 |
| ceil(x) |
任意 |
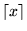 , ,  以上の最小の整数
(real part) 以上の最小の整数
(real part) |
| cos(x) |
任意 |
 のコサイン のコサイン 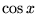 |
| cosh(x) |
任意 |
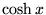 , ,  のハイパボリックコサイン のハイパボリックコサイン |
| erf(x) |
任意 |
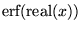 , ,  の 実部の誤差関数 の 実部の誤差関数 |
| erfc(x) |
任意 |
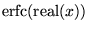 , 1.0 - ( , 1.0 - ( の実部の誤差関数) の実部の誤差関数) |
| exp(x) |
任意 |
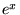 , ,  の指数関数 の指数関数 |
| floor(x) |
任意 |
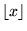 , ,  (の実部) 以下の最大の整数 (の実部) 以下の最大の整数 |
| gamma(x) |
任意 |
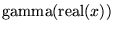 , ,  の実部のガンマ関数 の実部のガンマ関数 |
| ibeta(p,q,x) |
任意 |
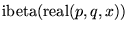 , , 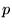 , ,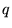 , , の実部の不完全ベータ関数 の実部の不完全ベータ関数 |
| inverf(x) |
任意 |
 の実部の逆誤差関数 の実部の逆誤差関数 |
| igamma(a,x) |
任意 |
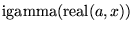 , , 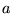 , , の実部の不完全ガンマ関数 の実部の不完全ガンマ関数 |
| imag(x) |
複素数 |
 の虚数部分 (実数) の虚数部分 (実数) |
| invnorm(x) |
任意 |
 の実部の逆正規分布関数 の実部の逆正規分布関数 |
| int(x) |
実数 |
 の実数部分 (0 に向かって丸め) の実数部分 (0 に向かって丸め) |
| lgamma(x) |
任意 |
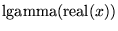 , ,  の実部のガンマ対数関数 の実部のガンマ対数関数 |
| log(x) |
任意 |
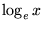 , ,  の自然対数 (底 の自然対数 (底 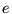 ) ) |
| log10(x) |
任意 |
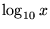 , ,  の対数 (底 の対数 (底 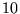 ) ) |
| norm(x) |
任意 |
 の実部の正規分布 (ガウス分布) 関数 の実部の正規分布 (ガウス分布) 関数 |
| rand(x) |
任意 |
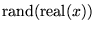 , 疑似乱数生成器 , 疑似乱数生成器 |
| real(x) |
任意 |
 の実部 の実部 |
| sgn(x) |
任意 |
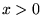 なら 1, なら 1, 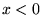 なら -1, なら -1, 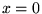 なら 0. なら 0.  の虚部は無視 の虚部は無視 |
| sin(x) |
任意 |
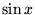 , ,  のサイン のサイン |
| sinh(x) |
任意 |
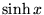 , ,  のハイパボリックサイン のハイパボリックサイン |
| sqrt(x) |
任意 |
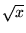 , ,  の平方根 の平方根 |
| tan(x) |
任意 |
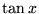 , ,  のタンジェント のタンジェント |
| tanh(x) |
任意 |
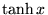 , ,  のハイパボリックタンジェント のハイパボリックタンジェント |
さらにいくつかの関数が追加されています。
| 他の gnuplot の関数 |
| 関数 |
引数 |
返り値 |
| column(x) |
整数 |
データファイル操作での  列目 列目 |
| tm_hour(x) |
整数 |
時 |
| tm_mday(x) |
整数 |
日 |
| tm_min(x) |
整数 |
分 |
| tm_mon(x) |
整数 |
月 |
| tm_sec(x) |
整数 |
秒 |
| tm_wday(x) |
整数 |
その週の何日目 |
| tm_yday(x) |
整数 |
その年の何日目 |
| tm_year(x) |
整数 |
西暦 |
| valid(x) |
整数 |
データ中の
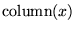 の正当性 の正当性 |



Next: 10.2 Operators
Up: 10 Expressions
Previous: 10 Expressions
Shigeharu TAKENO
2003年 10月 21日