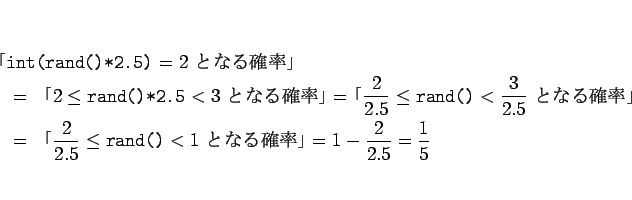次へ: 4.3 文字列値配列の生成
上へ: 4 課題文の作成
前へ: 4.1 乱数生成関数
(PDF ファイル: awk2.pdf)
4.2 ランダムな整数列
さて、0 以上 1 未満の乱数から、ランダムな文字列を生成するには
どうすればいいでしょうか。
これは、例えば次のようにすればできます。
- アルファベットの文字に
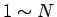 までの番号をつける
までの番号をつける
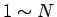 までの整数の乱数を 40 回作る
までの整数の乱数を 40 回作る
- その数字に対応する文字をひとつずつ並べた文字列を作る
rand() は 0 以上 1 未満の数を返すので、
例えばそれを 3 倍すれば 0 以上 3 未満の数になり、
その整数部分をとれば 0,1,2 の数がランダムに得られることになります。
整数部分を求める関数は int() で、
int(x):  の整数部分を返す
の整数部分を返す
となっています。よって、
x = int(rand()*3)
により、 に 0,1,2 のランダムな数が得られます。
に 0,1,2 のランダムな数が得られます。
なお、rand() を 2.5 倍したものは 0 以上 2.5 未満の数なので、
x = int(rand()*2.5)
でも  には 0,1,2 のランダムな数が得られますが、
これでは 0,1,2 の現れる確率が違ってしまいます。
には 0,1,2 のランダムな数が得られますが、
これでは 0,1,2 の現れる確率が違ってしまいます。
rand() は 0 以上 1 未満の「一様乱数」を生成するように設計されていますので、
rand() の 3 倍の値が
- 0 以上 1 未満 (整数部分は 0)
- 1 以上 2 未満 (整数部分は 1)
- 2 以上 3 未満 (整数部分は 2)
になる確率は等しく、それぞれ 1/3 となります。
ところが、rand() の 2.5 倍だと、
それは 0 以上 2.5 未満の一様乱数になりますので、
それが 2 以上 2.5 未満の値になる確率は、
0 以上 1 未満の値になる確率や
1 以上 2 未満の値になる確率の半分しかありません。
一般に、
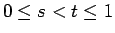 に対して、
rand() の値が
に対して、
rand() の値が 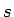 以上
以上 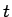 未満になる確率は
未満になる確率は 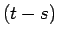 となります
3。
これを使って、x = int(rand()*2.5) が 2 となる確率を計算してみましょう。
となります
3。
これを使って、x = int(rand()*2.5) が 2 となる確率を計算してみましょう。
となります。
次へ: 4.3 文字列値配列の生成
上へ: 4 課題文の作成
前へ: 4.1 乱数生成関数
竹野茂治@新潟工科大学
2006年4月27日
の整数部分を返す
![]() に対して、
rand() の値が
に対して、
rand() の値が ![]() 以上
以上 ![]() 未満になる確率は
未満になる確率は ![]() となります
3。
これを使って、x = int(rand()*2.5) が 2 となる確率を計算してみましょう。
となります
3。
これを使って、x = int(rand()*2.5) が 2 となる確率を計算してみましょう。